题目内容
10.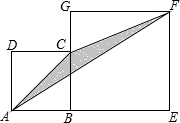 如图,四边形ABCD和四边形BEFG均为正方形,且A、B、E三点共线,正方形ABCD的边长为4,则S△ACF的面积为8.
如图,四边形ABCD和四边形BEFG均为正方形,且A、B、E三点共线,正方形ABCD的边长为4,则S△ACF的面积为8.
分析 首先根据相似三角形的性质得出QC的长,进而将阴影部分(△ACF)的面积分为S△AQC和S△FQC进而求出即可.
解答 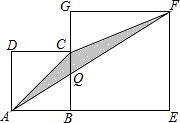 解:设正方形BEFG的边长为x,设AF与BC的交点为Q,
解:设正方形BEFG的边长为x,设AF与BC的交点为Q,
∵正方形ABCD为4,
∵在正方形BEFG中BG∥EF,
∴$\frac{AB}{AE}$=$\frac{BQ}{EF}$,
∴$\frac{4}{x+4}$=$\frac{BQ}{x}$,
解得:BQ=$\frac{4x}{x+4}$,
∴QC=4-$\frac{4x}{x+4}$=$\frac{16}{x+4}$,
∴图中阴影部分(△ACF)的面积是:$\frac{1}{2}$QC×AB+$\frac{1}{2}$QC×BE=$\frac{1}{2}$QC(AB+BE)=$\frac{1}{2}$×$\frac{16}{x+4}$×(4+x)=8.
故答案为:8.
点评 此题主要考查了正方形的性质以及相似三角形的性质和三角形面积求法等知识,根据已知得出QC的长是解题关键.

练习册系列答案
相关题目
18.设an=1+2+3+…+n,bn=12+22+32+…+n2,观察下表:
写出$\frac{{a}_{n}}{{b}_{n}}$与n的关系的等式:$\frac{{a}_{n}}{{b}_{n}}$=$\frac{3}{2n+1}$.
| n | 1 | 2 | 3 | 4 | 5 | … |
| an | 1 | 3 | 6 | 10 | 15 | … |
| bn | 1 | 5 | 14 | 30 | 55 | … |
19.直角三角形两直角边的和为6,则以此三角形的斜边为边长的正方形面积有( )
| A. | 最大值18 | B. | 最大值26 | C. | 最小值18 | D. | 最小值26 |
20.去年国庆假期,天安门接待游客日平均为10.7万人,这个假期7天共接待的游客人数用科学记数法可表示为( )
| A. | 1.07×105人 | B. | 7.49×104人 | C. | 7.49×105人 | D. | 7.49×106人 |
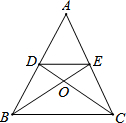 已知:如图,在△ABC中,AB=AC,点D、E分别在AB、AC上,
已知:如图,在△ABC中,AB=AC,点D、E分别在AB、AC上, 如图,Rt△ABC绕着点A顺时针旋转90°得到△AB′C′,若∠B=25°,∠C=90°.则∠BAC′的度数是25°.
如图,Rt△ABC绕着点A顺时针旋转90°得到△AB′C′,若∠B=25°,∠C=90°.则∠BAC′的度数是25°.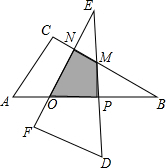 如图,在Rt△ABC中,已知:∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△DEF,则四边形MPQN的面积为$\frac{9}{4}$cm2.
如图,在Rt△ABC中,已知:∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△DEF,则四边形MPQN的面积为$\frac{9}{4}$cm2. 如图,一个正方形和一个长方形重叠在一起,重叠部分是边长为3的正方形,求阴影部分的面积.
如图,一个正方形和一个长方形重叠在一起,重叠部分是边长为3的正方形,求阴影部分的面积.