题目内容
7.已知在同一坐标系中,正比例函数y=kx(其中k≠0),反比例函数$y=\frac{t}{x}$(其中t≠0)的图象没有交点,试判断关于x的方程x2-ax+kt=0的根的情况并说明理由.分析 根据题意首先判断出kt<0,再判断△的值的情形即可解决问题.
解答 解:∵在同一坐标系中,y=kx(其中k≠0)和$y=\frac{t}{x}$(其中t≠0)的图象没有交点,
∴kt<0,
∵关于x的方程x2-ax+kt=0的根的判别式△=a2-4kt,
∴△>0,
∴关于x的方程x2-ax+kt=0有两个不相等的实数根.
点评 本题考查反比例函数与一次函数图象的交点、根的判别式等知识,解题的关键是灵活运用函数性质解决问题,记住根判别式△的值与一元二次方程的根关系,属于中考常考题型.

练习册系列答案
相关题目
18.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
请估计:
(1)当n很大时,摸到白球的频率将会接近0.6;(精确到0.1)
(2)假如你去摸一次,你摸到白球的概率是0.6,摸到黑球的概率是0.4;
(3)试估算口袋中黑球有多少只?
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数m | 58 | 96 | 116 | 295 | 484 | 601 |
| 摸到白球的频率$\frac{m}{n}$ | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(1)当n很大时,摸到白球的频率将会接近0.6;(精确到0.1)
(2)假如你去摸一次,你摸到白球的概率是0.6,摸到黑球的概率是0.4;
(3)试估算口袋中黑球有多少只?
2.某企业今年3月份产值为a万元,4月份比3月份减少了10%,5月份比4月份增加了15%,则5月份的产值是( )
| A. | (a-10%)(a+15%)万元 | B. | a(1-90%)(1+85%)万元 | C. | a(1-10%)(1+15%)万元 | D. | a(1-10%+15%)万元 |
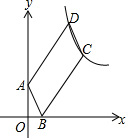 如图,在直角坐标系中,平行四边形ABCD的顶点A(0,2)、B(1,0)在x轴、y轴上,另两个顶点C、D在第一象限内,且AD=3AB.若反比例函数$y=\frac{k}{x}$(k>0)的图象经过C,D两点,则k的值是24.
如图,在直角坐标系中,平行四边形ABCD的顶点A(0,2)、B(1,0)在x轴、y轴上,另两个顶点C、D在第一象限内,且AD=3AB.若反比例函数$y=\frac{k}{x}$(k>0)的图象经过C,D两点,则k的值是24.