题目内容
7.设$\frac{\sqrt{2}+1}{\sqrt{2}-1}$的整数部分是x,小数部分是y(0<y<1),则x2+y2的值为37-8$\sqrt{2}$.分析 首先把$\frac{\sqrt{2}+1}{\sqrt{2}-1}$化为3+2$\sqrt{2}$,估算出3+2$\sqrt{2}$的大小,判断出x、y的值各是多少;然后把x、y的值代入,求出x2+y2的值为多少即可.
解答 解:$\frac{\sqrt{2}+1}{\sqrt{2}-1}$
=$\frac{{(\sqrt{2}+1)}^{2}}{(\sqrt{2}-1)(\sqrt{2}+1)}$
=3+2$\sqrt{2}$
∵1<$\sqrt{2}$<1.5,
∴2<2$\sqrt{2}$<3,
∴5<3+2$\sqrt{2}$<6,
∴x=5,y=3+2$\sqrt{2}$-5=2$\sqrt{2}$-2,
∴x2+y2
=52+${(2\sqrt{2}-2)}^{2}$
=25+12-8$\sqrt{2}$
=37-8$\sqrt{2}$
故答案为:37-8$\sqrt{2}$.
点评 此题主要考查了估算无理数的大小,要熟练掌握,解答此题的关键是估算出$\sqrt{2}$的大小.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
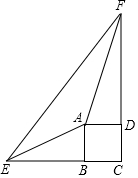 已知四边形ABCD是正方形,E、F分别在CB、CD的延长线上,∠EAF=135°.证明:BE+DF=EF.
已知四边形ABCD是正方形,E、F分别在CB、CD的延长线上,∠EAF=135°.证明:BE+DF=EF.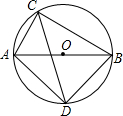 如图,AB为⊙O的直径,AC为⊙O的弦,AB=6,AC=2,∠ACB的平分线交⊙O于点D.
如图,AB为⊙O的直径,AC为⊙O的弦,AB=6,AC=2,∠ACB的平分线交⊙O于点D. ;
; .
.