题目内容
16.已知正比例函数y=4x与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,点A坐标为(1,m),反比例函数图象有一点P使得三角形ABP的面积为40,求P点坐标.分析 根据正比例函数y=4x与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,点A坐标为(1,m),求得m=4×1=4,k=1×4=4,进而得出反比例函数为y=$\frac{4}{x}$,再设点P(m,$\frac{4}{m}$),分两种情况进行讨论:①P在AB右侧,②P在AB左侧,分别构造矩形,根据割补法列出关于m的方程,求得m的值,即可得到P点坐标.
解答 解:∵正比例函数y=4x与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,点A坐标为(1,m),
∴m=4×1=4,k=1×4=4,
∴反比例函数为y=$\frac{4}{x}$,
设点P(m,$\frac{4}{m}$),
①当P在AB右侧时,如图所示,构造矩形BCDE,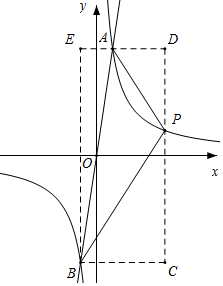
根据△ABP面积=矩形BCDE面积-△ABE面积-△BCP面积-△ADP面积,可得
8(m+1)-$\frac{1}{2}$×2×8-$\frac{1}{2}$×(m+1)×($\frac{4}{m}$+4)-$\frac{1}{2}$×(4-$\frac{4}{m}$)×(m-1)=40,
解得m=$\frac{5+3\sqrt{3}}{2}$或$\frac{5-3\sqrt{3}}{2}$,
∴$\frac{4}{m}$=-20+12$\sqrt{3}$或-20-12$\sqrt{3}$,
∴P($\frac{5+3\sqrt{3}}{2}$,-20+12$\sqrt{3}$)或($\frac{5-3\sqrt{3}}{2}$,-20-12$\sqrt{3}$);
②当P在AB左侧时,如图所示,构造矩形BCDE,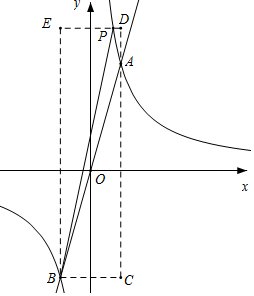
根据△ABP面积=矩形BCDE面积-△PBE面积-△BCA面积-△ADP面积,可得
2($\frac{4}{m}$+4)-$\frac{1}{2}$×(m+1)×($\frac{4}{m}$+4))-$\frac{1}{2}$×2×8-$\frac{1}{2}$×($\frac{4}{m}$-4)×(1-m)=40,
解得m=-5+$\sqrt{26}$或-5-$\sqrt{26}$,
∴$\frac{4}{m}$=20+4$\sqrt{26}$或20-4$\sqrt{26}$,
∴P(-5+$\sqrt{26}$,20+4$\sqrt{26}$)或(-5-$\sqrt{26}$,20-4$\sqrt{26}$).
点评 本题主要考查了反比例函数与一次函数交点的问题,解决问题的关键是作辅助线,构造矩形进行求解.解题时注意:若坐标平面内的三角形的各边与坐标轴都不垂直时,需要运用割补法求解.

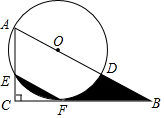 在Rt△ABC中,∠C=90°,D为AB边上的一点,以AD为直径的⊙O交AC于点E,交BC于点F,若F点恰好为$\widehat{DE}$的中点,连接EF、DF.
在Rt△ABC中,∠C=90°,D为AB边上的一点,以AD为直径的⊙O交AC于点E,交BC于点F,若F点恰好为$\widehat{DE}$的中点,连接EF、DF.
 如图,在△ABC中,AB=AC=20,BC=32,点D在边BC上,且∠CAD=90°,求BD的长.
如图,在△ABC中,AB=AC=20,BC=32,点D在边BC上,且∠CAD=90°,求BD的长.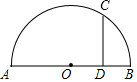 如图,AB是半圆O的直径,点C在半圆O上,CD⊥AB于D,AB=12,DB=4,求CD的长.
如图,AB是半圆O的直径,点C在半圆O上,CD⊥AB于D,AB=12,DB=4,求CD的长. -
- -
- )
)