题目内容
14.先化简,再求值:$({1+\frac{1}{{{x^2}-1}}})÷\frac{x^2}{x+1}$,其中x是一元二次方程x2-2x-2=0的正数解.分析 先求出一元二次方程x2-2x-2=0的解,再根据分式混合运算的法则把原式进行化简,把x的值代入进行计算即可.
解答 解:原式=$\frac{x^2}{{{x^2}-1}}•\frac{x+1}{x^2}$=$\frac{1}{x-1}$,
化简方程得,(x-1)2=3,
解方程得,${x_1}=1+\sqrt{3}$,${x_2}=1-\sqrt{3}$,
取正数解,则将$x=1+\sqrt{3}$代入原式,
原式=$\frac{{\sqrt{3}}}{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
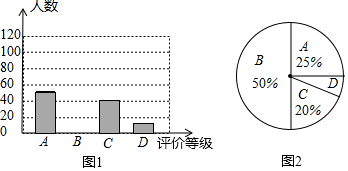
2. 为了了解大气污染情况,某学校兴趣小组搜集了2017年上半年中120天郑州市的空气质量指数,绘制了如下不完整的统计图表:
为了了解大气污染情况,某学校兴趣小组搜集了2017年上半年中120天郑州市的空气质量指数,绘制了如下不完整的统计图表:
空气质量指数统计表
请根据图表中提供的信息,解答下面的问题:
(1)空气质量指数统计表中的a=48,m=20%;
(2)请把空气质量指数条形统计图补充完整:
(3)若绘制“空气质量指数扇形统计图”,级别为“优”所对应扇形的圆心角是72度;
(4)请通过计算估计郑州市2017年(365天)中空气质量指数大于100的天数.
 为了了解大气污染情况,某学校兴趣小组搜集了2017年上半年中120天郑州市的空气质量指数,绘制了如下不完整的统计图表:
为了了解大气污染情况,某学校兴趣小组搜集了2017年上半年中120天郑州市的空气质量指数,绘制了如下不完整的统计图表:空气质量指数统计表
| 级别 | 指数 | 天数 | 百分比 |
| 优 | 0-50 | 24 | m |
| 良 | 51-100 | a | 40% |
| 轻度污染 | 101-150 | 18 | 15% |
| 中度污染 | 151-200 | 15 | 12.5% |
| 重度污染 | 201-300 | 9 | 7.5% |
| 严重污染 | 大于300 | 6 | 5% |
| 合计 | 120 | 100% |
(1)空气质量指数统计表中的a=48,m=20%;
(2)请把空气质量指数条形统计图补充完整:
(3)若绘制“空气质量指数扇形统计图”,级别为“优”所对应扇形的圆心角是72度;
(4)请通过计算估计郑州市2017年(365天)中空气质量指数大于100的天数.
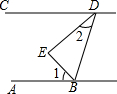 如图所示,BE是∠ABD的平分线,DE是∠BDC的平分线,且∠1+∠2=90°,那么直线AB、CD的位置关系如何?并说明理由.
如图所示,BE是∠ABD的平分线,DE是∠BDC的平分线,且∠1+∠2=90°,那么直线AB、CD的位置关系如何?并说明理由.
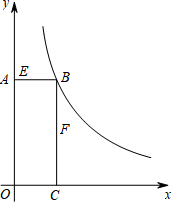 如图,矩形AOCB的顶点B在反比例函数$y=\frac{k}{x}(k>0$,x>0)的图象上,且AB=3,BC=8.若动点E从A开始沿AB向B以每秒1个单位长度的速度运动,同时动点F从B开始沿BC向C以每秒2个单位长度的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动,设运动时间为t秒.
如图,矩形AOCB的顶点B在反比例函数$y=\frac{k}{x}(k>0$,x>0)的图象上,且AB=3,BC=8.若动点E从A开始沿AB向B以每秒1个单位长度的速度运动,同时动点F从B开始沿BC向C以每秒2个单位长度的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动,设运动时间为t秒.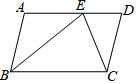 如图,在平行四边形ABCD中,E为AD上一点,AB=AE,CE=CD,若∠ECD=30°,则∠ABE=37.5°.
如图,在平行四边形ABCD中,E为AD上一点,AB=AE,CE=CD,若∠ECD=30°,则∠ABE=37.5°. 如图,在△ABC中,AB=13,BC=12,AC=5,CD=3,求△ABC的最大角及AD的长.
如图,在△ABC中,AB=13,BC=12,AC=5,CD=3,求△ABC的最大角及AD的长.