题目内容
6．
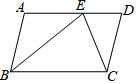如图，在平行四边形ABCD中，E为AD上一点，AB=AE，CE=CD，若∠ECD=30°，则∠ABE=37.5°．
分析 先根据等腰三角形的性质得出∠D的度数，再根据平行四边形的性质得出∠A的度数，再根据等腰三角形的性质得出∠ABE的度数，从而求解．
解答 解：∵CE=CD，∠ECD=30°，
∴∠D=$\frac{1}{2}$×（180°-30°）=75°，
∵四边形ABCD是平行四边形．
∴AB∥CD，
∴∠A+∠D=180°，
∴∠A=105°，
∵AB=AE，
∴∠ABE=$\frac{1}{2}$×（180°-105°）=37.5°．
故答案为：37.5°．
点评 本题考查了等腰三角形的性质及平行四边形的性质，根据题意得出∠A的度数是解答此题的关键．
练习册系列答案
相关题目
如图，已知在平面直角坐标系xOy中，O为坐标原点，点A，B分别在x轴上（点A在原点左侧，点B在原点右侧），OB=4OA，经过点A，B的抛物线交y轴于点C（0，2），且∠ACB=90°．
11．
为了解今年全县2000名初二学生“创新能力大赛”的笔试情况，随机抽取了部分同学的成绩，整理并制作如图所示的图表（部分未完成）．请你根据提供的信息，解答下列问题：
（1）此次调查的样本容量为400．
（2）在表中：m=160；n=0.3；h=0.4．
（3）补全频数分布直方图；
（4）根据频数分布表、频数分布直方图，你获得哪些信息？
为了解今年全县2000名初二学生“创新能力大赛”的笔试情况，随机抽取了部分同学的成绩，整理并制作如图所示的图表（部分未完成）．请你根据提供的信息，解答下列问题：（1）此次调查的样本容量为400．
（2）在表中：m=160；n=0.3；h=0.4．
（3）补全频数分布直方图；
（4）根据频数分布表、频数分布直方图，你获得哪些信息？
| 分数段 | 频数 | 频率 |
| 60≤x＜70 | 40 | 0.1 |
| 70≤x≤80 | 120 | n |
| 80≤x＜90 | m | h |
| 90≤x＜100 | 80 | 0.2 |
如图，C是线段AB上的一点，D是线段BC的中点，已知图中所有线段的长度之和为23.5，线段AC的长度与线段BC的长度都是正整数，则线段AC的长为2．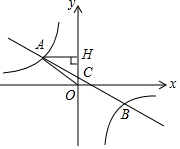
如图，在平面直角坐标系中，一次函数y=ax+b（a≠0）的图象与反比例函数y=$\frac{k}{x}$（k≠0）的图象交于第二、四象限内的A，B两点，与y轴交于C点，过点A作AH⊥y轴，垂足为H，OH=6，sin∠AOH=$\frac{4}{5}$，点B的坐标为（m，-4）．