题目内容
5．
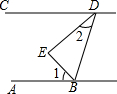如图所示，BE是∠ABD的平分线，DE是∠BDC的平分线，且∠1+∠2=90°，那么直线AB、CD的位置关系如何？并说明理由．
分析 首先根据角平分线的定义，可得：∠1=$\frac{1}{2}$∠ABD，∠2=$\frac{1}{2}$∠BDC，然后根据等量代换，求出∠ABD+∠BDC=180°，即可判断出AB∥CD．
解答 证明：直线AB、CD的位置关系为：AB∥CD，理由如下：
∵BE是∠ABD的平分线，DE是∠BDC的平分线，
∴∠1=$\frac{1}{2}$∠ABD，∠2=$\frac{1}{2}$∠BDC．
∵∠1+∠2=90°，
∴∠ABD+∠BDC=2（∠1+∠2）=2×90°=180°，
∴AB∥CD．
点评 此题主要考查了平行线的判定，解答此题的关键是熟练掌握角平分线定义和平行线的判定方法．
练习册系列答案
相关题目
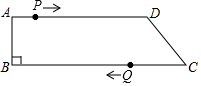如图，在四边形ABCD中，AD∥BC，∠B=90°，AB=8cm，AD=24cm，BC=30cm．点P从点A出发，以1cm/s的速度向点D移动，点Q从点C出发，以3cm/s的速度向点B运动，点P和点Q分别从点A和点C同时出发，移动时间为ts．规定若其中一个动点先到达端点（终点）时，另一个动点也随之停止运动．
如图，已知在平面直角坐标系xOy中，O为坐标原点，点A，B分别在x轴上（点A在原点左侧，点B在原点右侧），OB=4OA，经过点A，B的抛物线交y轴于点C（0，2），且∠ACB=90°．
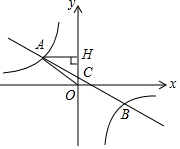如图，在平面直角坐标系中，一次函数y=ax+b（a≠0）的图象与反比例函数y=$\frac{k}{x}$（k≠0）的图象交于第二、四象限内的A，B两点，与y轴交于C点，过点A作AH⊥y轴，垂足为H，OH=6，sin∠AOH=$\frac{4}{5}$，点B的坐标为（m，-4）．