题目内容
5.函数y=$\frac{3}{2}$x+m与y=-$\frac{1}{2}$x+n均经过点A(-2,0),且与y轴交于B、C,则S△ABC=4.分析 可先根据点A的坐标用待定系数法求出a,b的值,即求出两个一次函数的解析式,进而求出它们与y轴的交点,即B,C的坐标.那么三角形ABC中,底边的长应该是B,C纵坐标差的绝对值,高就应该是A点横坐标的绝对值,因此可根据三角形的面积公式求出三角形的面积.
解答 解:把点A(-2,0)代入y=$\frac{3}{2}$x+m,
得:m=3,
∴点B(0,3).
把点A(-2,0)代入y=-$\frac{1}{2}$x+n,
得:n=-1,
∴点C(0,-1).
∴BC=|3-(-1)|=4,
∴S△ABC=$\frac{1}{2}$×2×4=4.
答:△ABC的面积为4,
故答案为:4.
点评 此题考查了用待定系数法求函数解析式以及一次函数与方程的关系,通过已知点的坐标来得出两函数的解析式是解题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
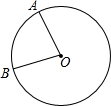 如图.点A、B把⊙O分成2:7两条弧,则∠AOB=80°.
如图.点A、B把⊙O分成2:7两条弧,则∠AOB=80°.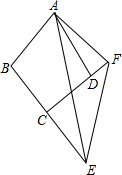 如图.在四边形ABCD中,∠B+∠ADC=180°,AB=AD,E、F分别是边BC、CD延长线上的点,且∠EAF=$\frac{1}{2}$∠BAD,求证:EF=BE-FD.
如图.在四边形ABCD中,∠B+∠ADC=180°,AB=AD,E、F分别是边BC、CD延长线上的点,且∠EAF=$\frac{1}{2}$∠BAD,求证:EF=BE-FD.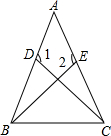 如图,在△ABC中,D,E分别是AB,AC上的点,且AD=AE,CD=BE,∠1=∠2.试判断△ABC的形状,并证明你的判断.
如图,在△ABC中,D,E分别是AB,AC上的点,且AD=AE,CD=BE,∠1=∠2.试判断△ABC的形状,并证明你的判断. 如图,正比例函数图象经过点A,将该图象向下平移2个单位后函数解析式是y=3x-2.
如图,正比例函数图象经过点A,将该图象向下平移2个单位后函数解析式是y=3x-2. 如图,花园中间有两条小路,小路的两个边界完全相同,且任何地方的水平宽度都相同,已知除去小路后的花园面积为600平方米.如果设计小路的宽度为x米,为求小路的宽度可列方程为x2-52x+40=0.
如图,花园中间有两条小路,小路的两个边界完全相同,且任何地方的水平宽度都相同,已知除去小路后的花园面积为600平方米.如果设计小路的宽度为x米,为求小路的宽度可列方程为x2-52x+40=0.