题目内容
13.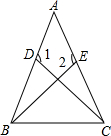 如图,在△ABC中,D,E分别是AB,AC上的点,且AD=AE,CD=BE,∠1=∠2.试判断△ABC的形状,并证明你的判断.
如图,在△ABC中,D,E分别是AB,AC上的点,且AD=AE,CD=BE,∠1=∠2.试判断△ABC的形状,并证明你的判断.
分析 由于AD=AE,CD=BE,∠1=∠2,根据全等三角形的判定方法得到△ABE≌△ACD,则AB=AC,得到△ABC是等腰三角形.
解答 解:△ABC是等腰三角形.理由如下:
在△ABE和△ACD中,
$\left\{\begin{array}{l}{AD=AE}\\{∠1=∠2}\\{CD=BE}\end{array}\right.$,
∴△ABE≌△ACD.
∴AB=AC.
∴△ABC是等腰三角形.
点评 本题考查了全等三角形的判定与性质:有两个边及其夹角对应相等的两个三角形全等;全等三角形的对应边相等.

练习册系列答案
相关题目
3.下面选项中是勾股数的一组是( )
| A. | 32,42,52 | B. | 20,28,35 | C. | 1.5,5,2.5 | D. | 7,24,25 |
8.菱形ABCD的对角线AC、BD交于点O,∠BAD=120°,AC=4,则它的面积是( )
| A. | 16 $\sqrt{3}$ | B. | 8 | C. | 16 | D. | 8 $\sqrt{3}$ |
18.购一批水果,运输过程中损失10%,不计其他费用,要想获得至少20%的利润,则售价至少比进价提高 ( )
| A. | 34% | B. | 33.4% | C. | 33.3% | D. | 33% |
 若用A、B、C分别表示有理数a、b、c,0为原点如图所示,化简:|c|+|a+b|+|b-c|-|a-c|.
若用A、B、C分别表示有理数a、b、c,0为原点如图所示,化简:|c|+|a+b|+|b-c|-|a-c|. 已知AB,CD相交于点O,且AB=CD,AD=CB,
已知AB,CD相交于点O,且AB=CD,AD=CB,