题目内容
20.若方程x2+(m2-1)x+m+$\frac{1}{2}$=0两根互为相反数,则m=-1.分析 根据根与系数的关系得m2-1=0,解得m1=1,m2=-1,然后根据根的判别式的意义确定满足条件的m的值.
解答 解:根据题意得m2-1=0,解得m1=1,m2=-1,
当m=1时,方程化为x2+$\frac{3}{2}$=0,方程没有实数解,
所以m的值为-1.
故答案为-1.
点评 若本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.

练习册系列答案
相关题目
8.菱形ABCD的对角线AC、BD交于点O,∠BAD=120°,AC=4,则它的面积是( )
| A. | 16 $\sqrt{3}$ | B. | 8 | C. | 16 | D. | 8 $\sqrt{3}$ |
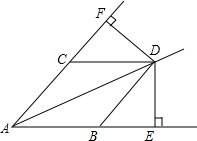 已知如图,点B、C在∠A的两边上,且AB=AC,D为∠CAB内的一点,DE⊥AB,DF⊥AC,垂足分别为E、F,DE=DF.
已知如图,点B、C在∠A的两边上,且AB=AC,D为∠CAB内的一点,DE⊥AB,DF⊥AC,垂足分别为E、F,DE=DF.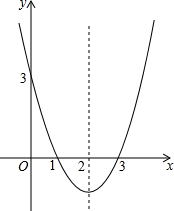 已知:抛物线y=ax2+bx+c的图象如图所示.
已知:抛物线y=ax2+bx+c的图象如图所示. 如图,所表示的是一个不等式的解集,则满足此解集的不等式可以为:x≥-2.
如图,所表示的是一个不等式的解集,则满足此解集的不等式可以为:x≥-2.