题目内容
16.已知关于x的分式方程$\frac{m}{x-2}$-$\frac{x+m}{x+2}$=1的解为正数,则m的取值范围是-$\frac{9}{8}$≤m<-1.分析 去分母将分式方程转化为整式方程x2-x-2-2m=0,根据关于x的分式方程$\frac{m}{x-2}$-$\frac{x+m}{x+2}$=1的解为正数,得出1-4(-2-2m)≥0,且-2-2m>0,求出m的范围,再将(x+2)(x-2)=0的m的值去掉即可.
解答 解:去分母得m(x+2)-(x+m)(x-2)=(x+2)(x-2),
整理,得x2-x-2-2m=0,
∵关于x的分式方程$\frac{m}{x-2}$-$\frac{x+m}{x+2}$=1的解为正数,
∴方程x2-x-2-2m=0的解为正数,
∴1-4(-2-2m)≥0,-2-2m>0,
∴-$\frac{9}{8}$≤m<-1,
∵x=2时,m=0;x=-2时,m=2,
∴-$\frac{9}{8}$≤m<-1,
故答案为:-$\frac{9}{8}$≤m<-1.
点评 本题考查了分式方程的解,一元一次不等式组的解法,理解解分式方程是转化为整式方程求解是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.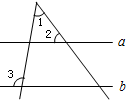 如图,直线a∥b,若∠1=50°,∠3=95°,则∠2的度数为( )
如图,直线a∥b,若∠1=50°,∠3=95°,则∠2的度数为( )
 如图,直线a∥b,若∠1=50°,∠3=95°,则∠2的度数为( )
如图,直线a∥b,若∠1=50°,∠3=95°,则∠2的度数为( )| A. | 35° | B. | 40° | C. | 45° | D. | 55° |
11. 六个大小相同的正方体搭成的几何体如图所示,其左视图是( )
六个大小相同的正方体搭成的几何体如图所示,其左视图是( )
 六个大小相同的正方体搭成的几何体如图所示,其左视图是( )
六个大小相同的正方体搭成的几何体如图所示,其左视图是( )| A. |  | B. |  | C. |  | D. |  |
1.小明买书需用34元钱,付款时恰好用了1元和5元的纸币共10张,设所用的1元纸币为x张,根据题意,下面所列方程正确的是( )
| A. | x+10(x-50)=34 | B. | x+5(10-x)=34 | C. | x+5(x-10)=34 | D. | 5x+(10-x)=34 |
8.在我县中学生春季田径运动会上,参加男子跳高的16名运动员的成绩如下表所示:
这些运动员跳高成绩的中位数和众数分别是( )
| 成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
| 人数 | 1 | 3 | 3 | 4 | 3 | 2 |
| A. | 1.70,1.65 | B. | 1.70,1.70 | C. | 1.65,1.70 | D. | 3,3 |
6.化简$\frac{a^2}{a-b}+\frac{b^2}{b-a}$的结果是( )
| A. | a+b | B. | b-a | C. | a-b | D. | -a-b |
 如图,已知△ABC与△BDE都是等边三角形,点D在边AC上(不与A、C重合),DE与AB相交于点F,则图中有( )对相似三角形(全等除外)
如图,已知△ABC与△BDE都是等边三角形,点D在边AC上(不与A、C重合),DE与AB相交于点F,则图中有( )对相似三角形(全等除外)