题目内容
2.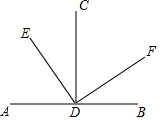 如图AB⊥CD.垂足为D,ED⊥DF,下列结论正确的有( )
如图AB⊥CD.垂足为D,ED⊥DF,下列结论正确的有( )(1)∠ADE=∠CDF(2)∠EDC=∠FDB(3)∠ADE与∠BDF互余(4)∠CDF与∠ADE互补.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据余角和补角的性质即可得到结论.
解答 解:∵AB⊥CD,ED⊥DF,
∴∠ADC=∠EDF=90°,
∴∠ADE+∠CDE=∠CDF+∠CDE=90°,
∴∠ADE=∠CDF,故(1)正确;
同理∠EDC=∠FDB,故(2)正确;
∵∠ADE+∠BDF=180°-∠EDF=180°-90°=90°,
∴∠ADE与∠BDF互余,故(3)正确;
∵∠CDF=∠ADE<90°,
∴∠CDF+∠ADE<180°,
∴∠CDF与∠ADE不互补,故(4)错误.
故选C.
点评 本题考查了余角和补角的性质,熟记余角和补角的性质是解题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
12. 如图所示,以BC为边的三角形共有( )
如图所示,以BC为边的三角形共有( )
 如图所示,以BC为边的三角形共有( )
如图所示,以BC为边的三角形共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.下列说法中,正确的是( )
| A. | 0是单项式 | B. | 单项式x2y的次数是2 | ||
| C. | 多项式ab+3是一次二项式 | D. | 单项式-$\frac{1}{3}$πx2y的系数是-$\frac{1}{3}$ |
10. 如图,在△ABC中,中线BE,CD相交于点O,连接DE,则下列判断错误的是( )
如图,在△ABC中,中线BE,CD相交于点O,连接DE,则下列判断错误的是( )
 如图,在△ABC中,中线BE,CD相交于点O,连接DE,则下列判断错误的是( )
如图,在△ABC中,中线BE,CD相交于点O,连接DE,则下列判断错误的是( )| A. | DE是△ABC的中位线 | B. | 点O是△ABC的重心 | ||
| C. | △DEO∽△CBO | D. | $\frac{{S}_{△DOE}}{{S}_{△ADE}}$=$\frac{1}{2}$ |
14.为了了解某班学生每天使用零花钱的情况,随机调查了15名同学,结果如下,下列说法正确的是( )
| 每天零花钱(元) | 0 | 5 | 10 | 15 | 20 |
| 人数 | 2 | 3 | 2 | 6 | 2 |
| A. | 众数是20元 | B. | 平均数是11元 | C. | 极差是15元 | D. | 中位数是10元 |
11. 六个大小相同的正方体搭成的几何体如图所示,其左视图是( )
六个大小相同的正方体搭成的几何体如图所示,其左视图是( )
 六个大小相同的正方体搭成的几何体如图所示,其左视图是( )
六个大小相同的正方体搭成的几何体如图所示,其左视图是( )| A. |  | B. |  | C. |  | D. |  |
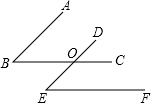 如图,已知AB∥DE,∠B=∠E,求证:BC∥EF.
如图,已知AB∥DE,∠B=∠E,求证:BC∥EF.