题目内容
9. 如图,⊙M与x轴相交于A(2,0)、B(8,0),与y轴相切于点C,P是优弧AB上的一点,则tan∠APB为( )
如图,⊙M与x轴相交于A(2,0)、B(8,0),与y轴相切于点C,P是优弧AB上的一点,则tan∠APB为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
分析 如图,作MN⊥AB于N,连接PA、PB、MA、MB、MC.首先证明四边形CONM是矩形,可得CM=AM=ON=5,在RtAMN中,MN=$\sqrt{{5}^{2}-{3}^{2}}$=4,由∠P=$\frac{1}{2}$∠AMB=∠AMN,推出tan∠APB=tan∠AMN=$\frac{AN}{MN}$=$\frac{3}{4}$.
解答 解:如图,作MN⊥AB于N,连接PA、PB、MA、MB、MC.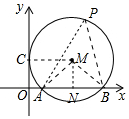
∵A(2,0),B(8,0),
∴OA=2,OB=8,AN=BN=3,
∵C是切点,
∴∠MCO=∠CON=∠MNO=90°,
∴四边形CONM是矩形,
∴CM=AM=ON=5,
在RtAMN中,MN=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∵∠P=$\frac{1}{2}$∠AMB=∠AMN,
∴tan∠APB=tan∠AMN=$\frac{AN}{MN}$=$\frac{3}{4}$.
故选B.
点评 本题考查切线的性质、圆周角定理、坐标与图形、解直角三角形、勾股定理等知识,解题的关键是掌握添加辅助线的方法,构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
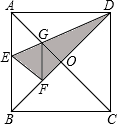 如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB,AC于点E、G,连接GF,有下列结论:
如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB,AC于点E、G,连接GF,有下列结论:
 如图:△ABC中,AB=AC,内切圆⊙O与边BC、AB分别切于点D、E、F,若∠C=30°,CE=2$\sqrt{3}$,则AC=4.
如图:△ABC中,AB=AC,内切圆⊙O与边BC、AB分别切于点D、E、F,若∠C=30°,CE=2$\sqrt{3}$,则AC=4.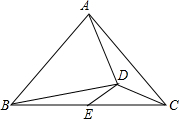 如图,在△ABC中,AB=AC,∠BAC=90°,点D在△ABC内部,AB=BD,AD=$\sqrt{2}$CD,E为BC边的中点,连接DE,若S△ACD=1,则线段DE的长为1.
如图,在△ABC中,AB=AC,∠BAC=90°,点D在△ABC内部,AB=BD,AD=$\sqrt{2}$CD,E为BC边的中点,连接DE,若S△ACD=1,则线段DE的长为1.