题目内容
20.不等式2x-6≥0的解集是x≥3.分析 首先移项,然后化系数为1即可求解.
解答 解:∵2x-6≥0,
∴2x≥6,
∴x≥3.
故答案为:x≥3.
点评 解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式,不等号的方向不变;(2)不等式的两边同时乘以或除以同一个正数,不等号的方向不变;(3)不等式的两边同时乘以或除以同一个负数,不等号的方向改变.

练习册系列答案
相关题目
11. 如图,已知正方形ABCD的边长为4,点E、F分别在边AB、ABC上,且AE=BF=1,CE、DF相交于点O,下列结论:
如图,已知正方形ABCD的边长为4,点E、F分别在边AB、ABC上,且AE=BF=1,CE、DF相交于点O,下列结论:
①∠DOC=90°,②OC=OE,③tan∠OCD=$\frac{4}{3}$,④△COD的面积等于四边形BEOF的面积,正确的有 ( )
 如图,已知正方形ABCD的边长为4,点E、F分别在边AB、ABC上,且AE=BF=1,CE、DF相交于点O,下列结论:
如图,已知正方形ABCD的边长为4,点E、F分别在边AB、ABC上,且AE=BF=1,CE、DF相交于点O,下列结论:①∠DOC=90°,②OC=OE,③tan∠OCD=$\frac{4}{3}$,④△COD的面积等于四边形BEOF的面积,正确的有 ( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5. 如图,已知平面直角坐标系中有点A(1,1),B(1,5),C(3,1),且双曲线y=$\frac{k}{x}$与△ABC有公共点,则k的取值范围是( )
如图,已知平面直角坐标系中有点A(1,1),B(1,5),C(3,1),且双曲线y=$\frac{k}{x}$与△ABC有公共点,则k的取值范围是( )
 如图,已知平面直角坐标系中有点A(1,1),B(1,5),C(3,1),且双曲线y=$\frac{k}{x}$与△ABC有公共点,则k的取值范围是( )
如图,已知平面直角坐标系中有点A(1,1),B(1,5),C(3,1),且双曲线y=$\frac{k}{x}$与△ABC有公共点,则k的取值范围是( )| A. | 1≤k≤3 | B. | 3≤k≤5 | C. | 1≤k≤5 | D. | 1≤k≤$\frac{49}{8}$ |
9. 如图,⊙M与x轴相交于A(2,0)、B(8,0),与y轴相切于点C,P是优弧AB上的一点,则tan∠APB为( )
如图,⊙M与x轴相交于A(2,0)、B(8,0),与y轴相切于点C,P是优弧AB上的一点,则tan∠APB为( )
 如图,⊙M与x轴相交于A(2,0)、B(8,0),与y轴相切于点C,P是优弧AB上的一点,则tan∠APB为( )
如图,⊙M与x轴相交于A(2,0)、B(8,0),与y轴相切于点C,P是优弧AB上的一点,则tan∠APB为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
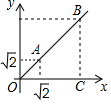 在平面直角坐标系中,点A($\sqrt{2}$,$\sqrt{2}$)、B(3$\sqrt{2}$,3$\sqrt{2}$ )动点C在x轴上,若以A、B、C三点为顶点的三角形是等腰三角形,则这样的点C有3个.
在平面直角坐标系中,点A($\sqrt{2}$,$\sqrt{2}$)、B(3$\sqrt{2}$,3$\sqrt{2}$ )动点C在x轴上,若以A、B、C三点为顶点的三角形是等腰三角形,则这样的点C有3个. 如图,在矩形ABCD中,O为AC中点,EF过点O且EF⊥AC分别交DC于点F,交AB于点E,点G是AE中点且∠AOG=30°,给出以下结论:
如图,在矩形ABCD中,O为AC中点,EF过点O且EF⊥AC分别交DC于点F,交AB于点E,点G是AE中点且∠AOG=30°,给出以下结论: 一个正方形的平面展开图如图所示,将它折成正方体后“建”字对面是安.
一个正方形的平面展开图如图所示,将它折成正方体后“建”字对面是安.