题目内容
19.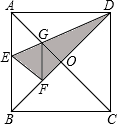 如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB,AC于点E、G,连接GF,有下列结论:
如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB,AC于点E、G,连接GF,有下列结论:①∠AGD=112.5°;②tan∠AED=$\sqrt{2}$+1;③四边形AEFG是菱形;④S△ACD=$\sqrt{3}$S△OCD.
其中正确结论的序号是①②③.(把所有正确结论的序号都填在横线上)
分析 根据翻转变换的性质、正方形的性质进行计算,判断即可.
解答 解:∵四边形ABCD是正方形,
∴∠ADB=45°,
由折叠的性质可知,∠ADE=∠BDE=22.5°,
∴∠AGD=180°-90°-22.5°=112.5°,①正确;
设AE=x,
∵△BEF是等腰直角三角形,
∴BE=$\sqrt{2}$EF=$\sqrt{2}$AE=$\sqrt{2}$x,
∴x+$\sqrt{2}$x=1,
解得,x=$\sqrt{2}$-1,
∴tan∠AED=$\frac{AD}{AE}$=$\sqrt{2}$+1,②正确;
由同位角相等可知,GF∥AB,EF∥AC,
∴四边形AEFG是平行四边形,
由折叠的性质可知,EA=EF,
∴四边形AEFG是菱形,③正确;
由正方形的性质可知,S△ACD=2S△OCD,④错误,
故答案为:①②③.
点评 本题考查的是翻转变换的性质、菱形的性质、解直角三角形的应用,掌握翻转变换是一种对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.

练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
14.二次函数y=x2-2x的顶点为( )
| A. | (1,1) | B. | (2,-4) | C. | (-1,1) | D. | (1,-1) |
4.对于反比例函数y=-$\frac{3}{x}$,下列说法不正确的是( )
| A. | 图象经过点(1,-3) | |
| B. | 图象分布在第二、四象限 | |
| C. | 当x>0时,y随x的增大而增大 | |
| D. | 点A(x1,y1)、B(x2、y2)都在反比例函数y=-$\frac{3}{x}$的图象上,若x1<x2,则y1<y2 |
11. 如图,已知正方形ABCD的边长为4,点E、F分别在边AB、ABC上,且AE=BF=1,CE、DF相交于点O,下列结论:
如图,已知正方形ABCD的边长为4,点E、F分别在边AB、ABC上,且AE=BF=1,CE、DF相交于点O,下列结论:
①∠DOC=90°,②OC=OE,③tan∠OCD=$\frac{4}{3}$,④△COD的面积等于四边形BEOF的面积,正确的有 ( )
 如图,已知正方形ABCD的边长为4,点E、F分别在边AB、ABC上,且AE=BF=1,CE、DF相交于点O,下列结论:
如图,已知正方形ABCD的边长为4,点E、F分别在边AB、ABC上,且AE=BF=1,CE、DF相交于点O,下列结论:①∠DOC=90°,②OC=OE,③tan∠OCD=$\frac{4}{3}$,④△COD的面积等于四边形BEOF的面积,正确的有 ( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9. 如图,⊙M与x轴相交于A(2,0)、B(8,0),与y轴相切于点C,P是优弧AB上的一点,则tan∠APB为( )
如图,⊙M与x轴相交于A(2,0)、B(8,0),与y轴相切于点C,P是优弧AB上的一点,则tan∠APB为( )
 如图,⊙M与x轴相交于A(2,0)、B(8,0),与y轴相切于点C,P是优弧AB上的一点,则tan∠APB为( )
如图,⊙M与x轴相交于A(2,0)、B(8,0),与y轴相切于点C,P是优弧AB上的一点,则tan∠APB为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |