题目内容
3.已知不等式:①x<3 ②x2≤0 ③3≤x≤4 ④x≥3中,其解集中只有一个实数的是②(只填序号)分析 逐一分析四个不等式解集中实数的个数,由此即可得出结论.
解答 解:①x<3,实数的个数有无数个;
②x2≤0,即x=0,实数的个数有一个;
③3≤x≤4,实数的个数有无数个;
④x≥3,实数的个数有无数个.
故答案为:②.
点评 本题考查了不等式的解集,逐一分析四个不等式解集中实数的个数是解题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
9. 如图,⊙M与x轴相交于A(2,0)、B(8,0),与y轴相切于点C,P是优弧AB上的一点,则tan∠APB为( )
如图,⊙M与x轴相交于A(2,0)、B(8,0),与y轴相切于点C,P是优弧AB上的一点,则tan∠APB为( )
 如图,⊙M与x轴相交于A(2,0)、B(8,0),与y轴相切于点C,P是优弧AB上的一点,则tan∠APB为( )
如图,⊙M与x轴相交于A(2,0)、B(8,0),与y轴相切于点C,P是优弧AB上的一点,则tan∠APB为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
8.若x>y,则下列式子错误的是( )
| A. | x+2>y+2 | B. | -2x<-2y | C. | 1-x>1-y | D. | $\frac{x}{2}>\frac{y}{2}$ |
15.下列关于平方根的说法,错误的是( )
| A. | $\frac{1}{64}$的算术平方根是$\frac{1}{8}$ | B. | -3是9的一个平方根 | ||
| C. | 13是(-13)2的算术平方根 | D. | 0.4的算术平方根是0.02 |
 一个正方形的平面展开图如图所示,将它折成正方体后“建”字对面是安.
一个正方形的平面展开图如图所示,将它折成正方体后“建”字对面是安.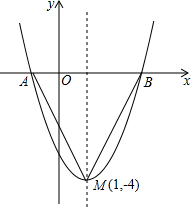 如图:二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4).
如图:二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4).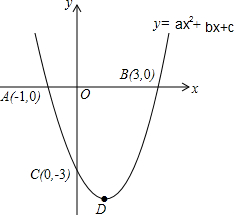 已知抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,与y轴交于点C,点B和点C的坐标分别为(3,0)(0,-3),抛物线的对称轴为x=1,D为抛物线 的顶点.
已知抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,与y轴交于点C,点B和点C的坐标分别为(3,0)(0,-3),抛物线的对称轴为x=1,D为抛物线 的顶点.