题目内容
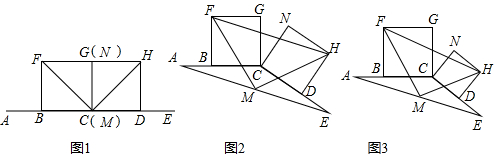
在图1至图3中,点B是线段AC的中点,点D是线段CE的中点.四边形BCGF和CDHN都是正方形.AE的中点是M,FH的中点是P.
(1)如图1,点A、C、E在同一条直线上,根据图形填空:
①△BMF是 三角形;
②MP与FH的位置关系是 ,MP与FH的数量关系是 ;
(2)将图1中的CE绕点C顺时针旋转一个锐角,得到图2,解答下列问题:
①证明:△BMF是等腰三角形;
②(1)中得到的MP与FH的位置关系与数量关系的结论是否仍然成立?证明你的结论;
(3)将图2中的CE缩短到图3的情况,(2)中的三个结论还成立吗?(成立的不需要说明理由,不成立的需要说明理由)
(1)如图1,点A、C、E在同一条直线上,根据图形填空:
①△BMF是
②MP与FH的位置关系是
(2)将图1中的CE绕点C顺时针旋转一个锐角,得到图2,解答下列问题:
①证明:△BMF是等腰三角形;
②(1)中得到的MP与FH的位置关系与数量关系的结论是否仍然成立?证明你的结论;
(3)将图2中的CE缩短到图3的情况,(2)中的三个结论还成立吗?(成立的不需要说明理由,不成立的需要说明理由)

考点:全等三角形的判定与性质,等腰三角形的判定与性质,三角形中位线定理
专题:
分析:(1)根据正方形的性质可得FB=BM=MD=DH,然后利用“边角边”证明△FBM和△MDH全等,根据全等三角形对应边相等可得FM=MH,再求出∠FMH=90°,得到FM⊥HM,然后根据等腰直角三角形的定义证明即可;
(2)连接MB、MD,设FM与AC交于点Q,根据三角形的中位线平行于第三边并且等于第三边的一半可得MD∥BC,且MD=BC=BF;MB∥CD,且MB=CD=DH,然后得到四边形BCDM是平行四边形并求出∠CBM=∠CDM,再求出∠FBM=∠MDH,然后利用“边角边”证明△FBM和△MDH全等,根据全等三角形对应边相等可得FM=MH,全等三角形对应角相等可得∠MFB=∠HMD,根据两直线平行,内错角相等可得∠AQM=∠FMD,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠FMH=∠FBQ=90°,再根据等腰直角三角形的定义证明即可;
(3)证明方法同(2).
(2)连接MB、MD,设FM与AC交于点Q,根据三角形的中位线平行于第三边并且等于第三边的一半可得MD∥BC,且MD=BC=BF;MB∥CD,且MB=CD=DH,然后得到四边形BCDM是平行四边形并求出∠CBM=∠CDM,再求出∠FBM=∠MDH,然后利用“边角边”证明△FBM和△MDH全等,根据全等三角形对应边相等可得FM=MH,全等三角形对应角相等可得∠MFB=∠HMD,根据两直线平行,内错角相等可得∠AQM=∠FMD,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠FMH=∠FBQ=90°,再根据等腰直角三角形的定义证明即可;
(3)证明方法同(2).
解答: 解:(1)△FMH是等腰直角三角形.
解:(1)△FMH是等腰直角三角形.
∵四边形BCGF和CDHN都是正方形,点N与点G重合,点M与点C重合,
∴FB=BM=MD=DH,∠FBM=∠MDH=90°,
在△FBM和△MDH中,
,
∴△FBM≌△MDH(SAS),
∴FM=MH,
∵∠FMB=∠DMH=45°,
∴∠FMH=90°,
∴FM⊥HM,
∴△FMH是等腰直角三角形;
②∵△FMH是等腰直角三角形,P是斜边FH的中线,
∴MP⊥FH,MP=
FH,

(2)①△FMH是等腰直角三角形,
连接MB、MD,如图2,设FM与AC交于点Q.
∵B、D、M分别是AC、CE、AE的中点,
∴MD∥BC,且MD=BC=BF;MB∥CD,且MB=CD=DH,
∴四边形BCDM是平行四边形,
∴∠CBM=∠CDM,
又∵∠FBC=∠HDC,
∴∠FBM=∠MDH,
在△FBM和△MDH中,
,
∴△FBM≌△MDH(SAS),
∴FM=MH,且∠MFB=∠HMD,
∵BC∥MD,
∴∠AQM=∠FMD,
∴∠FMH=∠FMD-∠HMD=∠AQM-∠MFB=∠FBC=90°,
∴△FMH是等腰直角三角形;
②仍然成立;
∵△FMH是等腰直角三角形,P是斜边FH的中线,
∴MP⊥FH,MP=
FH,

(3)三个结论还成立;
连接MB、MD,如图3,设FM与AC交于点P.
∵B、D、M分别是AC、CE、AE的中点,
∴MD∥BC,且MD=BC=BF;MB∥CD,且MB=CD=DH,
∴四边形BCDM是平行四边形,
∴∠CBM=∠CDM,
又∵∠FBP=∠HDC,
∴∠FBM=∠MDH,
在△FBM和△MDH中,
,
∴△FBM≌△MDH(SAS),
∴FM=MH,且∠MFB=∠HMD,
∵BC∥MD,
∴∠APM=∠FMD,
∴∠FMH=∠FMD-∠HMD=∠APM-∠MFB=∠FBP=90°,
∴△FMH是等腰直角三角形.
∵是斜边FH的中线,
∴MP⊥FH,MP=
FH;
 解:(1)△FMH是等腰直角三角形.
解:(1)△FMH是等腰直角三角形.∵四边形BCGF和CDHN都是正方形,点N与点G重合,点M与点C重合,
∴FB=BM=MD=DH,∠FBM=∠MDH=90°,
在△FBM和△MDH中,
|
∴△FBM≌△MDH(SAS),
∴FM=MH,
∵∠FMB=∠DMH=45°,
∴∠FMH=90°,
∴FM⊥HM,
∴△FMH是等腰直角三角形;
②∵△FMH是等腰直角三角形,P是斜边FH的中线,
∴MP⊥FH,MP=
| 1 |
| 2 |

(2)①△FMH是等腰直角三角形,
连接MB、MD,如图2,设FM与AC交于点Q.
∵B、D、M分别是AC、CE、AE的中点,
∴MD∥BC,且MD=BC=BF;MB∥CD,且MB=CD=DH,
∴四边形BCDM是平行四边形,
∴∠CBM=∠CDM,
又∵∠FBC=∠HDC,
∴∠FBM=∠MDH,
在△FBM和△MDH中,
|
∴△FBM≌△MDH(SAS),
∴FM=MH,且∠MFB=∠HMD,
∵BC∥MD,
∴∠AQM=∠FMD,
∴∠FMH=∠FMD-∠HMD=∠AQM-∠MFB=∠FBC=90°,
∴△FMH是等腰直角三角形;
②仍然成立;
∵△FMH是等腰直角三角形,P是斜边FH的中线,
∴MP⊥FH,MP=
| 1 |
| 2 |

(3)三个结论还成立;
连接MB、MD,如图3,设FM与AC交于点P.
∵B、D、M分别是AC、CE、AE的中点,
∴MD∥BC,且MD=BC=BF;MB∥CD,且MB=CD=DH,
∴四边形BCDM是平行四边形,
∴∠CBM=∠CDM,
又∵∠FBP=∠HDC,
∴∠FBM=∠MDH,
在△FBM和△MDH中,
|
∴△FBM≌△MDH(SAS),
∴FM=MH,且∠MFB=∠HMD,
∵BC∥MD,
∴∠APM=∠FMD,
∴∠FMH=∠FMD-∠HMD=∠APM-∠MFB=∠FBP=90°,
∴△FMH是等腰直角三角形.
∵是斜边FH的中线,
∴MP⊥FH,MP=
| 1 |
| 2 |
点评:本题考查了全等三角形的判定与性质,正方形的性质,三角形的中位线平行于第三边并且等于第三边的一半,平行四边形的判定与性质,熟记性质并作辅助线构造出全等三角形和平行四边形的解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 如图,正方形ABCD的边长为1,点F在线段CD上运动,AE平分∠BAF交BC边于点E.
如图,正方形ABCD的边长为1,点F在线段CD上运动,AE平分∠BAF交BC边于点E.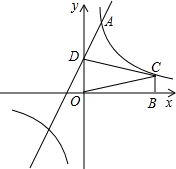 如图,已知平面直角坐标系xOy中,直线y=k1x+2与反比例函数
如图,已知平面直角坐标系xOy中,直线y=k1x+2与反比例函数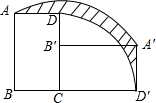 如图,矩形ABCD中,AB=8,BC=6,现将此矩形绕点C顺时针旋转90°得到新的矩形A′B′CD′,则边AD扫过的面积(阴影部分)是
如图,矩形ABCD中,AB=8,BC=6,现将此矩形绕点C顺时针旋转90°得到新的矩形A′B′CD′,则边AD扫过的面积(阴影部分)是