题目内容
 如图,正方形ABCD的边长为1,点F在线段CD上运动,AE平分∠BAF交BC边于点E.
如图,正方形ABCD的边长为1,点F在线段CD上运动,AE平分∠BAF交BC边于点E.(1)过A作AG⊥AF,交CB延长线于点G,求证:①AG=AF,②AF=DF+BE;
(2)延长AF交BC延长线于点H,若AE=EH,求此时DF的长.
考点:正方形的性质,全等三角形的判定与性质
专题:
分析:(1)①利用正方形的性质和已知条件可证明:△ABG≌△ADF,由全等三角形的性质即可得到AG=AF;②由①可知:∠GAB=∠DAF,GB=DF,所以∠GAE=∠DAE,在正方形ABCD中,因为AD∥BC,所以∠DAE=∠BEA,进而可得∠GAE=∠BEA,所以AG=GE,所以AF=GB+BE问题得证;
(2)若AE=EH,则可证明出∠DAF=∠FAE=∠BAE=
×90°=30°,利用30°角的正切值即可求出DF的长.
(2)若AE=EH,则可证明出∠DAF=∠FAE=∠BAE=
| 1 |
| 3 |
解答:解:(1)①∵四边形ABCD是正方形,
∴AB=DA,∠ABG=∠D=∠BAD=90°,
∴∠DAF+∠BAF=90°,
又∵AG⊥AF,
∴∠GAB+∠BAF=90°,
∴∠GAB=∠DAF,
在△ABG和△ADF中,
,
∴△ABG≌△ADF(ASA),
∴AG=AF;
②∵AE平分∠BAF,
∴∠BAE=∠FAE,
∵△ABG≌△ADF,
∴∠GAB=∠DAF,GB=DF,
∴∠GAE=∠DAE,
在正方形ABCD中,AD∥BC,
∴∠DAE=∠BEA,
∴∠GAE=∠BEA,
∴AG=GE,
∵AG=AF,
∴GE=AF,
∴AF=GB+BE,
∴AF=DF+BE;
(2)∵AD∥BC,
∴∠H=∠DAF,
∵AE=EH,
∴∠H=∠FAE,
∵∠BAE=∠FAE,
∴∠DAF=∠FAE=∠BAE=
×90°=30°,
在Rt△ADF中,tan∠DAF=
,
即tan30°=
=
,
∴DF=
.
∴AB=DA,∠ABG=∠D=∠BAD=90°,
∴∠DAF+∠BAF=90°,
又∵AG⊥AF,
∴∠GAB+∠BAF=90°,
∴∠GAB=∠DAF,
在△ABG和△ADF中,
|
∴△ABG≌△ADF(ASA),
∴AG=AF;
②∵AE平分∠BAF,
∴∠BAE=∠FAE,
∵△ABG≌△ADF,
∴∠GAB=∠DAF,GB=DF,
∴∠GAE=∠DAE,
在正方形ABCD中,AD∥BC,
∴∠DAE=∠BEA,
∴∠GAE=∠BEA,
∴AG=GE,
∵AG=AF,
∴GE=AF,
∴AF=GB+BE,
∴AF=DF+BE;
(2)∵AD∥BC,
∴∠H=∠DAF,
∵AE=EH,
∴∠H=∠FAE,
∵∠BAE=∠FAE,
∴∠DAF=∠FAE=∠BAE=
| 1 |
| 3 |
在Rt△ADF中,tan∠DAF=
| DF |
| AD |
即tan30°=
| DF |
| 1 |
| ||
| 3 |
∴DF=
| ||
| 3 |
点评:本题考查了正方形的性质、全等三角形的判定和性质、等腰三角形的判定和性质、平行线的性质,题目的综合性很强,难度也不小,解答(2)中时求出∠DAF=∠FAE=∠BAE=
×90°=30°,是解题的关键.
| 1 |
| 3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
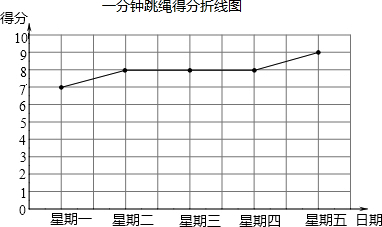 我市体育中考规定:可以在立定跳远和1分钟跳绳中任选一项测试,同学们将根据自己平时的运动成绩确定自己的报考项目,下面是小亮同学在近期的两个项目中连续五次测试的得分情况(立定跳远得分统计表和1分钟跳绳得分折线图).
我市体育中考规定:可以在立定跳远和1分钟跳绳中任选一项测试,同学们将根据自己平时的运动成绩确定自己的报考项目,下面是小亮同学在近期的两个项目中连续五次测试的得分情况(立定跳远得分统计表和1分钟跳绳得分折线图).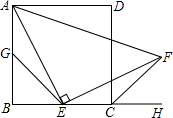 如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.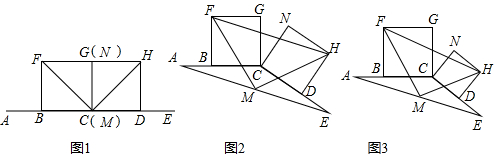
 如图,双曲线y=
如图,双曲线y= 直角三角形在正方形网格纸中的位置如图,则tanα=
直角三角形在正方形网格纸中的位置如图,则tanα=