题目内容
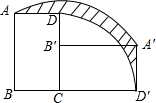如图，矩形ABCD中，AB=8，BC=6，现将此矩形绕点C顺时针旋转90°得到新的矩形A′B′CD′，则边AD扫过的面积（阴影部分）是考点：扇形面积的计算,矩形的性质,旋转的性质
专题：
分析：连接AC、A′C，则阴影部分的面积为扇形ACA′的面积减去扇形CDD′的面积．
解答：
解：连接AC、AC′，
根据勾股定理，得AC=
=10，
故可得S扇形CAA'=
=25π，
S扇形CDD'=
=18π，
则阴影部分的面积=S扇形CAA'-S扇形CDD'=25π-18π=7π．
故答案为7π．
解：连接AC、AC′，根据勾股定理，得AC=
| AB2+BC2 |
故可得S扇形CAA'=
| 90π×CA2 |
| 360 |
S扇形CDD'=
| 90πCD2 |
| 360 |
则阴影部分的面积=S扇形CAA'-S扇形CDD'=25π-18π=7π．
故答案为7π．
点评：本题考查了扇形的面积公式和旋转的旋转以及勾股定理，能够把不规则图形的面积转换为规则图形的面积．
练习册系列答案
相关题目
如图，双曲线y=
直角三角形在正方形网格纸中的位置如图，则tanα=
如图，在平面直角坐标中，四边形OABC是正方形，顶点A，C在坐标轴上，以边AB为弦的⊙M与x轴相切，若点A（0，8），则经过圆心M的反比例函数的解析式为．
如图，AB是⊙O的直径，弦CD⊥AB，∠C=30°，CD=2一种细菌的直径是0.000016m，用科学记数法应记为（ ）
| A、1.6×10-7m |
| B、1.6×10-6m |
| C、1.6×10-5m |
| D、16×10-6m |