题目内容
8.反比例函数y=$\frac{k}{x}$的图象经过点A(2,-3).(1)求这个函数的解析式;
(2)请判断点B(-5,1)是否在这个反比例函数的图象上,并说明理由.
分析 (1)把点A的坐标代入函数解析式来求k的值;
(2)把点B的坐标代入函数解析式进行验证.
解答 解:(1)∵反比例函数y=$\frac{k}{x}$的图象经过点A(2,-3),
∴-3=$\frac{k}{2}$,
解得 k=-6.
则该函数解析式为:y=-$\frac{6}{x}$;
(2)点B(-5,1)是不在这个反比例函数的图象上,理由如下:
由(1)知,函数解析式为:y=-$\frac{6}{x}$.
∵当x=-5时,y=-$\frac{6}{-5}$=$\frac{6}{5}$≠1,
∴点B(-5,1)是不在这个反比例函数的图象上.
点评 本题考查了待定系数法求反比例函数解析式,反比例函数图象上点的坐标特征.经过函数的某点一定在函数的图象上.

练习册系列答案
相关题目
19.定义符号max{a,b}的含义为:当a≥b时max{a,b}=a;当a<b时,max{a,b}=b.如:max{1,-5}=1,max{-3,-4}=-3.则max{x2+x-2,-x}的最小值是( )
| A. | -1+$\sqrt{3}$ | B. | -1-$\sqrt{3}$ | C. | 1-$\sqrt{3}$ | D. | 1+$\sqrt{3}$ |
13.已知直线y=x+1与反比例函数y=$\frac{k}{x}$的图象的一个交点为P(a,2),则ak的值为( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | -$\frac{1}{2}$ |
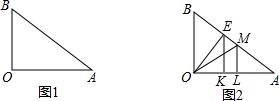 如图1,已知Rt△AOB中,∠AOB=90°,AO=5,BO=3,
如图1,已知Rt△AOB中,∠AOB=90°,AO=5,BO=3,