题目内容
 如图,在△ABC中,AB=AC,E是BC上一点,D是AC上一点,且AE=AD,若∠DEC=20°,求∠BAE的度数.
如图,在△ABC中,AB=AC,E是BC上一点,D是AC上一点,且AE=AD,若∠DEC=20°,求∠BAE的度数.考点:等腰三角形的性质
专题:
分析:根据等腰三角形的性质得出∠B=∠C,∠ADE=∠AED,设∠C=∠B=x,则∠ADE=∠AED=20+x,根据三角形的内角和即可求得∠BAE的度数.
解答:解:∵AB=AC,
∴∠B=∠C,
∵AE=AD,
∴∠ADE=∠AED,
设∠C=∠B=x,则∠ADE=∠AED=20+x,
∴∠EAD=180-(20+x+20+x)=140-2x,
∴∠BAE=180-x-x-(140-2x)=40,
∴∠BAE=40°.
∴∠B=∠C,
∵AE=AD,
∴∠ADE=∠AED,
设∠C=∠B=x,则∠ADE=∠AED=20+x,
∴∠EAD=180-(20+x+20+x)=140-2x,
∴∠BAE=180-x-x-(140-2x)=40,
∴∠BAE=40°.
点评:本题考查了等腰三角形的性质,三角形外角的性质,三角形的内角和定理,熟练掌握性质定理是解题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
如果3am+1b2与-
ab2n-2是同类项,则m-n为( )
| 1 |
| 2 |
| A、2 | B、-2 | C、1 | D、-1 |
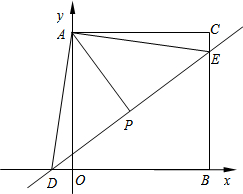 如图,平面直角坐标系中,过点C(28,28)分别作x轴、y轴的垂线,垂足分别为B、A,一次函数y=
如图,平面直角坐标系中,过点C(28,28)分别作x轴、y轴的垂线,垂足分别为B、A,一次函数y=