题目内容
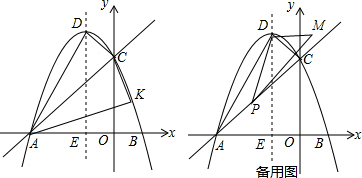
5.平面直角坐标系中,抛物线y=ax2+bx+c交x轴于A,B两点(点A在点B左侧),与y轴交于点C,点A,C的坐标分别为(-3,0),(0,3),对称轴直线x=-1交x轴于点E,点D为顶点.(1)求抛物线的解析式;
(2)点K是直线AC下方的抛物线上一点,且S△KAC=S△DAC求点K的坐标;
(3)如图2若点P是线段AC上的一个动点,∠DPM=30°,DP⊥DM,则点P的线段AC上运动时,D点不变,M点随之运动,求当点P从点A运动到点C时,点M运动的路径长.
分析 (1)根据条件可得到关于a、b、c的三元一次方程组,只需解这个方程组就可解决问题;
(2)过点D作DH⊥y轴于H,连接EK交y轴于F,连接EC,如图1,运用割补法可求出△DAC的面积,易得S△ADC=S△AEC,由S△KAC=S△DAC,可得S△KAC=S△EAC,从而可得EK∥AC,根据平行线分线段成比例可求出OF,然后运用待定系数法可求出直线EK的解析式,只需求出直线EK与抛物线的交点坐标就可解决问题;
(3)设点P在点A处时点M在点M′,点P在点C处时点M在点M″,如图2.易证△DPC∽△DMM″,△DAC∽△DM′M″,从而可得∠DM″M=∠DM″M′=∠DCP,由于∠DCP是定值,因此点M的运动路径是线段M′M″,然后只需根据△DM′M″∽△DAC,运用相似三角形的性质就可解决问题.
解答 解:(1)由题意可得,
$\left\{\begin{array}{l}{9a-3b+c=0}\\{c=3}\\{-\frac{b}{2a}=-1}\end{array}\right.$
解得$\left\{\begin{array}{l}{a=-1}\\{b=-2}\\{c=3}\end{array}\right.$,
∴抛物线的解析式为y=-x2-2x+3;
(2)过点D作DH⊥y轴于H,连接EK交y轴于F,连接EC,如图1.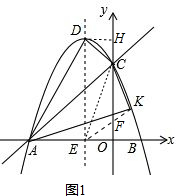
由y=-x2-2x+3=-(x+1)2+4可得顶点D为(-1,4),
∴S△ADC=S梯形AOHD-S△OAC-S△DHC
=$\frac{1}{2}$(1+3)×4-$\frac{1}{2}$×3×3-$\frac{1}{2}$×1×(4-3)=3.
又∵S△AEC=$\frac{1}{2}$AE•OC=$\frac{1}{2}$×2×3=3,
∴S△ADC=S△AEC.
∵S△KAC=S△DAC,
∴S△KAC=S△EAC,
∴EK∥AC,
∴$\frac{OF}{OC}=\frac{OE}{OA}$,
∴$\frac{OF}{3}=\frac{1}{3}$,
∴OF=1,F(0,1).
设直线EK的解析式为y=mx+n,则有
$\left\{\begin{array}{l}{-m+n=0}\\{n=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=1}\\{n=1}\end{array}\right.$,
∴直线EK的解析式为y=x+1.
解方程组$\left\{\begin{array}{l}{y=x+1}\\{y=-{x}^{2}-2x+3}\end{array}\right.$,得
$\left\{\begin{array}{l}{{x}_{1}=\frac{-3+\sqrt{17}}{2}}\\{{y}_{1}=\frac{-1+\sqrt{17}}{2}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\frac{-3-\sqrt{17}}{2}}\\{{y}_{2}=\frac{-1-\sqrt{17}}{2}}\end{array}\right.$,
∴点K的坐标为($\frac{-3+\sqrt{17}}{2}$,$\frac{-1+\sqrt{17}}{2}$)或($\frac{-3-\sqrt{17}}{2}$,$\frac{-1-\sqrt{17}}{2}$);
(3)设点P在点A处时点M在点M′,点P在点C处时点M在点M″,如图2.
∵∠CDM″=∠PDM=90°,∠DPM=∠DCM″=30°,
∴$\frac{DM}{DP}=\frac{DM″}{DC}$=$\frac{\sqrt{3}}{3}$,∠PDC=∠MDM″,
∴△DPC∽△DMM″,
∴∠DCP=∠DM″M.
同理可得△DAC∽△DM′M″,
∴∠DCA=∠DM″M′.
∴∠DM″M=∠DM″M′=∠DCP,
∵∠DCP是定值,
∴点M的运动路径是线段M′M″.
∵△DM′M″∽△DAC,
∴$\frac{M′M″}{AC}$=$\frac{DM″}{DC}$=$\frac{\sqrt{3}}{3}$.
∵AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
∴M′M″=$\sqrt{6}$,
∴点M的运动路径长为$\sqrt{6}$.
点评 本题主要考查了运用待定系数法求二次函数及一次函数的解析式、相似三角形的判定与性质、求直线与抛物线的交点坐标、平行线分线段成比例、勾股定理等知识,运用割补法及逆用平行等积法是解决第(2)小题的关键,确定点M的运动路径是解决第(3)小题的关键.

 智慧小复习系列答案
智慧小复习系列答案| A. | y=(x+1)2+2 | B. | y=(x-1)2-2 | C. | y=(x+1)2-2 | D. | y=(x-1)2+2 |
 如图,一圆柱高为8cm,底面周长为30cm,蚂蚁在圆柱表面爬行,从点A爬到点B的最短路程是( )
如图,一圆柱高为8cm,底面周长为30cm,蚂蚁在圆柱表面爬行,从点A爬到点B的最短路程是( )| A. | 15cm | B. | 17cm | C. | 18cm | D. | 30cm |
| 销售量(x台) | 每台奖励金额(元) |
| 0<x≤100 | 200 |
| 100<x≤300 | 500 |
| x>300 | 1000 |
(2)在新办法出台前一个月,该经销商销售的A型和B型汽车分别为多少台?
(3)若A型汽车每台售价为10万元,B型汽车每台售价为12万元.新奖励办法是:每销售一台A型汽车按每台汽车售价的a%给予奖励,每销售一台B型汽车按每台汽车售价的(a+0.2)%给予奖励.新奖励办法出台后的第二个月,A型汽车的销售量比出台后的第一个月增加了10a%; 而B型汽车受到某问题零件召回的影响,销售量比出台后的第一个月减少了20a%,新奖励办法出台后的第二个月该经销商共获得的奖励金额355680元,求a的值.
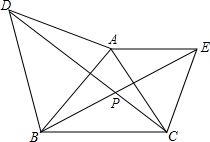 如图,△ABC中,分别以AB、AC为边向外作正△ABD、△ACE.试说明:
如图,△ABC中,分别以AB、AC为边向外作正△ABD、△ACE.试说明: