题目内容
9.已知x=$\frac{1}{\sqrt{3}}$,求$\frac{\sqrt{{x}^{2}-2x+1}}{{x}^{2}-x}$-$\frac{1-2x+{x}^{2}}{x-1}$的值.分析 首先化简二次根式,然后把分式进行化简,然后代入数值即可计算.
解答 解:x=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$<1,
原式=$\frac{\sqrt{(x-1)^{2}}}{x(x-1)}$-$\frac{(x-1)^{2}}{x-1}$
=$\frac{1-x}{x(x-1)}$-(x-1)
=-$\frac{1}{x}$-x+1,
当x=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$时,原式=-$\sqrt{3}$-$\frac{\sqrt{3}}{3}$+1=1-$\frac{4\sqrt{3}}{3}$.
点评 本题考查了二次根式的化简求值,注意化简二次根式是解决本题的关键.

练习册系列答案
相关题目
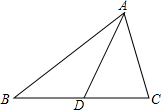 如图,AD为△ABC中BC边上的中线,试说明S△ABD=S△ADC.
如图,AD为△ABC中BC边上的中线,试说明S△ABD=S△ADC.