题目内容
18.已知一元二次方程x2+bx+c=0的两根分别是2+$\sqrt{3}$和2-$\sqrt{3}$,则b、c的值为( )| A. | 4、1 | B. | -4、1 | C. | -4、-1 | D. | 4、-1 |
分析 由于x的一元二次方程x2+bx+c=0的两根分别为2+$\sqrt{3}$和2-$\sqrt{3}$,利用根与系数的关系,即可求得b与c的值.
解答 解:∵一元二次方程x2+bx+c=0的两根分别为2+$\sqrt{3}$和2-$\sqrt{3}$,
∴x1+x2=-b=2+$\sqrt{3}$+2-$\sqrt{3}$=4,x1•x2=c=(2+$\sqrt{3}$)(2-$\sqrt{3}$)=1,
∴b=-4,c=1.
故选B.
点评 此题考查了根与系数的关系.此题比较简单,注意掌握若二次项系数为1,x1,x2是方程x2+px+q=0的两根时,则x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
10.将一元二次方程3x2+4x=7化成一般式后,一次项系数和常数项分别为( )
| A. | 4,7 | B. | -4,7 | C. | 4,-7 | D. | -4,-7 |
8.下列命题中,真命题是( )
| A. | 两组数据1、2、3、4、5与21、22、23、24、25的离散程度相同 | |
| B. | 若点C是线段AB的黄金分割点,且AB=10,则AC≈6.18 | |
| C. | 等腰三角形的边长是方程x2-6x+8=0的两个解,则这个三角形的底边长为2或4 | |
| D. | 在平行光线的照射下,不同物体的物高与影长成比例 |
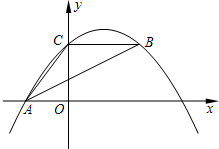 如图,抛物线y=(m-1)x2+(5-5m)x+4经过△ABC的三个顶点,点A在x轴上,点C在y轴上,B与C是抛物线的对称点,AB平分∠CAO.
如图,抛物线y=(m-1)x2+(5-5m)x+4经过△ABC的三个顶点,点A在x轴上,点C在y轴上,B与C是抛物线的对称点,AB平分∠CAO. 如图,正方形ABCD中,E是CD中点,$FC=\frac{1}{4}BC$,则tan∠EAF=$\frac{1}{2}$.
如图,正方形ABCD中,E是CD中点,$FC=\frac{1}{4}BC$,则tan∠EAF=$\frac{1}{2}$.