题目内容
7.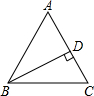 如图,△ABC中,∠ABC:∠C=5:7,∠C比∠A大10°,BD是△ABC的高,求∠A与∠CBD的度数.
如图,△ABC中,∠ABC:∠C=5:7,∠C比∠A大10°,BD是△ABC的高,求∠A与∠CBD的度数.
分析 由∠ABC:∠C=5:7,设∠ABC=5x,∠C=7x,然后由∠C比∠A大10°,可得:∠A=7x-10,然后根据三角形内角和定理可求∠A和∠C的度数,然后由BD是△ABC的高,可得:∠BDC=90°,然后根据三角形内角和定理可求∠CBD的度数.
解答 解:∵∠ABC:∠C=5:7,
∴设∠ABC=5x,∠C=7x,
∵∠C比∠A大10°,
∴∠A=7x-10,
∵∠A+∠ABC+∠C=180°,
即:7x-10+5x+7x=180°,
解得:x=10,
∴∠C=7x=70°,∠A=7x-10=60°,
∵BD是△ABC的高,
∴∠BDC=90°,
∵∠BDC+∠C+∠CBD=180°,
∴∠CBD=20°.
点评 此题考查了三角形内角和定理:三角形内角和为180°.解题的关键是:根据三角形内角和定理求出∠A和∠C的度数.

练习册系列答案
相关题目
2.下列说法中正确的个数是2.
(1)长度相等的两条弧是等弧;
(2)半径相等的两个半圆是等弧;
(3)同圆中,优弧与劣弧的和等于一个整圆;
(4)分别在两个等圆上两条弧是等弧;
(5)能够完全重合的弧是等弧.
(1)长度相等的两条弧是等弧;
(2)半径相等的两个半圆是等弧;
(3)同圆中,优弧与劣弧的和等于一个整圆;
(4)分别在两个等圆上两条弧是等弧;
(5)能够完全重合的弧是等弧.
7.下列二次根式中,不能再化简的是( )
| A. | $\sqrt{14}$ | B. | $\sqrt{\frac{1}{3}}$ | C. | $\sqrt{8}$ | D. | $\sqrt{0.2}$ |
 如图,在△ABC中,AB=AC,D、E、F分别在三边上,且BE=CD,BD=CF,G为EF的中点.
如图,在△ABC中,AB=AC,D、E、F分别在三边上,且BE=CD,BD=CF,G为EF的中点. 如图,点N(0,6),点M在x轴负半轴上,ON=3OM,A为线段MN上一点,AB⊥x轴,垂足为B,AC⊥y轴,垂足为C,AB=$\frac{1}{3}$ON.
如图,点N(0,6),点M在x轴负半轴上,ON=3OM,A为线段MN上一点,AB⊥x轴,垂足为B,AC⊥y轴,垂足为C,AB=$\frac{1}{3}$ON.
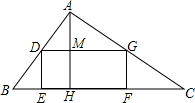 如图,矩形DEFG内接于Rt△ABC,∠BAC=90°,AH是斜边上的高,BH=1,AH=2.
如图,矩形DEFG内接于Rt△ABC,∠BAC=90°,AH是斜边上的高,BH=1,AH=2.