题目内容
 如图,在Rt△ABC 中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将
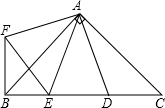
如图,在Rt△ABC 中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF.
(1)求证:∠EAF=45°;
(2)求证:EF=DE;
(3)求证:BE2+DC2=DE2.
考点:旋转的性质,全等三角形的判定与性质,勾股定理
专题:证明题
分析:(1)根据旋转的性质可得∠FAD=90°,然后根据∠FAE=90°-∠DAE代入数据计算即可得解;
(2)根据旋转变换只改变图形的位置不改变图形的形状可得△ADC和△AFB全等,根据全等三角形对应边相等可得AD=AF,然后利用“边角边”证明△AED和△AEF全等,根据全等三角形对应边相等可得EF=DE;
(3)求出∠FBE=90°,再利用勾股定理列式整理即可得证.
(2)根据旋转变换只改变图形的位置不改变图形的形状可得△ADC和△AFB全等,根据全等三角形对应边相等可得AD=AF,然后利用“边角边”证明△AED和△AEF全等,根据全等三角形对应边相等可得EF=DE;
(3)求出∠FBE=90°,再利用勾股定理列式整理即可得证.
解答:证明:(1)∵△ADC绕点A顺时针旋转90°得△AFB,
∴∠FAD=90°,
又∵∠DAE=45°,
∴∠FAE=90°-∠DAE=45°;
(2)∵△ADC绕点A顺时针旋转90°得△AFB,
∴△ADC≌△AFB,
∴AD=AF,
在△AED和△AEF中,
,
∴△AED≌△AEF(SAS),
∴EF=DE;
(3)在Rt△ABC中,∠ABC+∠ACB=90°,
又∵△ADC≌△AFB,
∴∠ACB=∠ABF,CD=BF,
∴∠ABC+∠ABF=90°,
即∠FBE=90°,
在Rt△FBE中,BE2+BF2=FE2,
∴BE2+DC2=DE2.
∴∠FAD=90°,
又∵∠DAE=45°,
∴∠FAE=90°-∠DAE=45°;
(2)∵△ADC绕点A顺时针旋转90°得△AFB,
∴△ADC≌△AFB,
∴AD=AF,
在△AED和△AEF中,
|
∴△AED≌△AEF(SAS),
∴EF=DE;
(3)在Rt△ABC中,∠ABC+∠ACB=90°,
又∵△ADC≌△AFB,
∴∠ACB=∠ABF,CD=BF,
∴∠ABC+∠ABF=90°,
即∠FBE=90°,
在Rt△FBE中,BE2+BF2=FE2,
∴BE2+DC2=DE2.
点评:本题考查了旋转的性质,全等三角形的判定与性质,勾股定理的应用,熟记性质并准确识图,理清图中各角度和边之间的关系是解题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
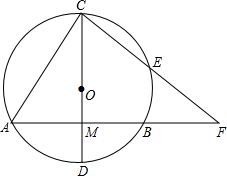 如图,⊙O的弦AB=8,直径CD⊥AB于M,OM:MD=3:2,E是劣弧CB上一点,连结CE并延长交CE的延长线于点F.求:
如图,⊙O的弦AB=8,直径CD⊥AB于M,OM:MD=3:2,E是劣弧CB上一点,连结CE并延长交CE的延长线于点F.求: 如图,方格纸中每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点在格点上.且A(1,-4),B(5,-4),C(4,-1)
如图,方格纸中每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点在格点上.且A(1,-4),B(5,-4),C(4,-1)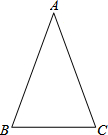 如图,在△ABC中,已知∠B=∠C.
如图,在△ABC中,已知∠B=∠C.