题目内容
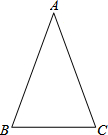如图，在△ABC中，已知∠B=∠C．（1）尺规作图：作底角∠ABC的平分线BD，交AC于点D（作图不写作法，但保留作图痕迹）；
（2）猜想：“若∠A=36°，则△ABD和△BDC都是等腰三角形”．请你通过计算说明猜想是否成立．
考点：作图—基本作图,等腰三角形的判定
专题：
分析：（1）利用尺规作图平分已知角即可；
（2）利用等腰三角形的性质及角平分线的性质分别得到AD=DB，BD=BC即可得到等腰三角形．
（2）利用等腰三角形的性质及角平分线的性质分别得到AD=DB，BD=BC即可得到等腰三角形．
解答：
解：（1）如图所示：BD即为所求；
（2）∵∠A=36°，
∴∠ABC=∠C=（180°-36°）÷2=72°，
∵BD平分∠ABC，
∴∠ABD=∠DBC=72°÷2=36°，
∴∠CDB=180°-36°-72°=72°，
∵∠A=∠ABD=36°，∠C=∠CDB=72°，
∴AD=DB，BD=BC，
∴△ABD和△BDC都是等腰三角形．
解：（1）如图所示：BD即为所求；（2）∵∠A=36°，
∴∠ABC=∠C=（180°-36°）÷2=72°，
∵BD平分∠ABC，
∴∠ABD=∠DBC=72°÷2=36°，
∴∠CDB=180°-36°-72°=72°，
∵∠A=∠ABD=36°，∠C=∠CDB=72°，
∴AD=DB，BD=BC，
∴△ABD和△BDC都是等腰三角形．
点评：本题考查了基本作图中的平分已知角及等腰三角形的判定的知识，属于基础题，难度不大．
练习册系列答案
相关题目
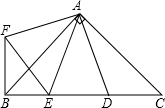如图，在Rt△ABC 中，AB=AC，D、E是斜边BC上两点，且∠DAE=45°，将
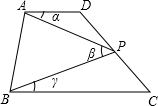如图，已知四边形ABCD，AD∥BC．点P在直线CD上运动（点P和点C，D不重合，点P，A，B不在同一条直线上），若记∠DAP，∠APB，∠PBC分别为∠α，∠β，∠γ．
如图，菱形ABCD，四个顶点分别是A（-2，-1），B（1，-3），C（4，-1），D（1，1）．将菱形沿y轴正方向平移3个单位长度，各个顶点的坐标变为多少？画出平移后的图形．