题目内容
某工厂计划生产两种产品共10件,其生产成本和利润如下表:
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂投入资金不多于44万元,且获利多于14万元,问工厂会有哪几种生产方案?请说明理由.
| A种产品 | B种产品 | |
| 成本(万元∕件) | 2 | 5 |
| 利润(万元∕件) | 1 | 3 |
(2)若工厂投入资金不多于44万元,且获利多于14万元,问工厂会有哪几种生产方案?请说明理由.
考点:一元一次不等式组的应用,一元一次方程的应用
专题:
分析:1)设生产A种产品x件,则生产B种产品有(10-x)件,根据计划获利14万元,即两种产品共获利14万元,即可列方程求解;
(2)根据计划投入资金不多于44万元,且获利多于14万元,这两个不等关系即可列出不等式组,求得x的范围,再根据x是非负整数,确定x的值,x的值的个数就是方案的个数.
(2)根据计划投入资金不多于44万元,且获利多于14万元,这两个不等关系即可列出不等式组,求得x的范围,再根据x是非负整数,确定x的值,x的值的个数就是方案的个数.
解答:解:(1)设生产A种产品x件,则生产B种产品(10-x)件,于是有
x+3(10-x)=14,
解得:x=8,
则10-x=10-8=2(件)
所以应生产A种产品8件,B种产品2件;
(2)设应生产A种产品x件,则生产B种产品有(10-x)件,由题意有:
,
解得:2≤x<8;
所以可以采用的方案有:
,
,
,
,
,
,共6种方案.
x+3(10-x)=14,
解得:x=8,
则10-x=10-8=2(件)
所以应生产A种产品8件,B种产品2件;
(2)设应生产A种产品x件,则生产B种产品有(10-x)件,由题意有:
|
解得:2≤x<8;
所以可以采用的方案有:
|
|
|
|
|
|
点评:本题考查了一元一次方程的应用,一元一次不等式组的应用.解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的数量关系.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目

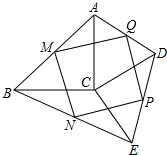 如图,在△ABC和△DCE中,BC=AC,DC=CE,∠ACB=∠DCE=90°,且AB,BD,DE,EA的中点分别是点M,N,P,Q.求证:四边形MNPQ是菱形.
如图,在△ABC和△DCE中,BC=AC,DC=CE,∠ACB=∠DCE=90°,且AB,BD,DE,EA的中点分别是点M,N,P,Q.求证:四边形MNPQ是菱形. 如图,在△ABC中,∠C=120°,∠A=∠B,BC的垂直平分线交AB于E,交BC于D,若DE=2,求AB的长.
如图,在△ABC中,∠C=120°,∠A=∠B,BC的垂直平分线交AB于E,交BC于D,若DE=2,求AB的长. 如图,给下列条件:
如图,给下列条件:
 如图,△ABC按逆时针方向旋转一个角度后成为△AED,且∠BAD=120°,则旋转中心为
如图,△ABC按逆时针方向旋转一个角度后成为△AED,且∠BAD=120°,则旋转中心为