题目内容
有一张长方形纸片ABCD,如图(1),将它折叠,使AD边落在AB边上,折痕为AE,如图(2);再将∠A折叠,使点A与点B重合,折痕为MN,如图(3).如果AD=4cm,MD=1cm,那么DB= cm.

考点:翻折变换(折叠问题)
专题:
分析:利用折叠的性质,可得BM=
AB=
(AD+BD)=BD+MD,由此代入数值即可求得答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:由折叠可知:
BM=
AB=
(AD+BD)=BD+MD,
又∵AD=4cm,MD=1cm,
∴
(4+BD)=BD+1
解得BD=2.
故答案为:2.
BM=
| 1 |
| 2 |
| 1 |
| 2 |
又∵AD=4cm,MD=1cm,
∴
| 1 |
| 2 |
解得BD=2.
故答案为:2.
点评:此题考查了折叠的性质,找出线段之间的数量关系是解决问题的关键,注意数形结合思想的应用.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目

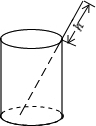 如图,一根长18cm的筷子置于底面半径为5cm.高为12cm圆柱形水杯中,露在水杯外面的长度hcm,则h的取值范围是
如图,一根长18cm的筷子置于底面半径为5cm.高为12cm圆柱形水杯中,露在水杯外面的长度hcm,则h的取值范围是 如图,在△ACE和△DBF中,点A,B,C,D在一条直线上,∠A=∠D,AE=DF.在下列条件中随机抽取一个作为补充条件:①∠E=∠F;②AB=CD;③CE=BF;④CE∥BF.能使△ACE≌△DBF的概率是
如图,在△ACE和△DBF中,点A,B,C,D在一条直线上,∠A=∠D,AE=DF.在下列条件中随机抽取一个作为补充条件:①∠E=∠F;②AB=CD;③CE=BF;④CE∥BF.能使△ACE≌△DBF的概率是 如图,在菱形ABCD中,AC,BD是对角线,如果∠BAC=70°,那么∠ADC等于
如图,在菱形ABCD中,AC,BD是对角线,如果∠BAC=70°,那么∠ADC等于