题目内容
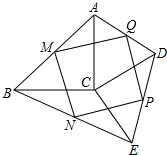 如图,在△ABC和△DCE中,BC=AC,DC=CE,∠ACB=∠DCE=90°,且AB,BD,DE,EA的中点分别是点M,N,P,Q.求证:四边形MNPQ是菱形.
如图,在△ABC和△DCE中,BC=AC,DC=CE,∠ACB=∠DCE=90°,且AB,BD,DE,EA的中点分别是点M,N,P,Q.求证:四边形MNPQ是菱形.考点:中点四边形
专题:证明题
分析:首先连接AC,BD,利用三角形的中位线定理证得四边形MNPQ是平行四边形,然后证得△BCE≌△ACD后证得MN=NQ,利用邻边相等的平行四边形是菱形判定结论即可.
解答: 证明:连接AC,BD,
证明:连接AC,BD,
∵AB,BD,DE,EA的中点分别是点M,N,P,Q,
∴MN∥AD,PQ∥AD,MQ∥BE,NP∥BE,MN=
AD,MQ=
BE
∴MN∥PQ,MQ∥NP,
∴四边形MNPQ是平行四边形,
在△BCE和△ACD中,
,
∴△BCE≌△ACD(SAS),
∴BE=AD,
∴MN=NQ,
∴平行四边形MNPQ是菱形.
 证明:连接AC,BD,
证明:连接AC,BD,∵AB,BD,DE,EA的中点分别是点M,N,P,Q,
∴MN∥AD,PQ∥AD,MQ∥BE,NP∥BE,MN=
| 1 |
| 2 |
| 1 |
| 2 |
∴MN∥PQ,MQ∥NP,
∴四边形MNPQ是平行四边形,
在△BCE和△ACD中,
|
∴△BCE≌△ACD(SAS),
∴BE=AD,
∴MN=NQ,
∴平行四边形MNPQ是菱形.
点评:本题考查了中点四边形的知识,解题的关键是正确的构造辅助线和了解菱形的判定定理,难度中等.

练习册系列答案
相关题目
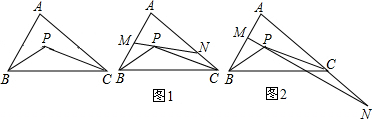
 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3),△AOB关于y轴对称的图形为△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3),△AOB关于y轴对称的图形为△A1OB1.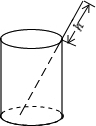 如图,一根长18cm的筷子置于底面半径为5cm.高为12cm圆柱形水杯中,露在水杯外面的长度hcm,则h的取值范围是
如图,一根长18cm的筷子置于底面半径为5cm.高为12cm圆柱形水杯中,露在水杯外面的长度hcm,则h的取值范围是