题目内容
 如图,在△ABC中,∠C=120°,∠A=∠B,BC的垂直平分线交AB于E,交BC于D,若DE=2,求AB的长.
如图,在△ABC中,∠C=120°,∠A=∠B,BC的垂直平分线交AB于E,交BC于D,若DE=2,求AB的长.考点:线段垂直平分线的性质
专题:
分析:连接CE,根据三角形的内角和定理求出∠A、∠B,再根据线段垂直平分线上的点到两端点的距离相等可得BE=CE,根据等边对等角可得∠ECB=∠B=30°,再根据直角三角形30°角所对的直角边等于斜边的一半解答.
解答: 解:如图,连接CE,
解:如图,连接CE,
∵∠C=120°,∠A=∠B,
∴∠A=∠B=
(180°-120°)=30°,
∵BC的垂直平分线交AB,
∴BE=CE,∠BDE=90°,
∴∠ECB=∠B=30°,
∴BE=2DE=2×2=4,
∵∠ACE=∠ACB-∠BCE=120°-30°=90°,
∴AE=2CE=2×4=8,
∴AB=AE+BE=8+4=12.
 解:如图,连接CE,
解:如图,连接CE,∵∠C=120°,∠A=∠B,
∴∠A=∠B=
| 1 |
| 2 |
∵BC的垂直平分线交AB,
∴BE=CE,∠BDE=90°,
∴∠ECB=∠B=30°,
∴BE=2DE=2×2=4,
∵∠ACE=∠ACB-∠BCE=120°-30°=90°,
∴AE=2CE=2×4=8,
∴AB=AE+BE=8+4=12.
点评:本题考查了线段垂直平分线上的点到两端点的距离相等的性质,等边对等角的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,熟记各性质并求出含30°角的直角三角形是解题的关键.

练习册系列答案
相关题目
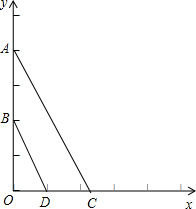 已知:如图,在平面直角坐标系xOy中,A(0,4),B(0,2),点C在x轴的正半轴上,点D为OC的中点.
已知:如图,在平面直角坐标系xOy中,A(0,4),B(0,2),点C在x轴的正半轴上,点D为OC的中点. 两个边长为a的正方形和两个长为a,宽为b的长方形如图摆放组成一个大长方形;通过计算该图形的面积知,该图形可表示的代数恒等式是
两个边长为a的正方形和两个长为a,宽为b的长方形如图摆放组成一个大长方形;通过计算该图形的面积知,该图形可表示的代数恒等式是