题目内容
16.已知在直角坐标系中,△ABC的顶点A(-2,0),B(2,4),C(5,0).(1)求△ABC的面积;
(2)点D为y轴负半轴上一动点,连BD交x轴于E,是否存在点D,使得S△ADE=S△BCE?若存在,请求出点D的坐标;若不存在,请说明理由.
分析 (1)根据三角形的面积公式,即可解答;
(2)存在,过点C作AB的平行线交y轴负半轴的点即为符合条件的点D,根据等底等高面积相等,得到S△ADC=S△BDC,所以S△ADC-S△DCE=S△BDC-S△DCE,即S△ADE=S△BCE,利用△ABF是等腰直角三角形,证明△OCD是等腰直角三角形即可解答.
解答 解:(1)如图1,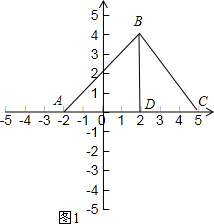
∵△ABC的顶点A(-2,0),B(2,4),C(5,0),
∴AC=7,BD=4,
∴${S}_{△ABC}=\frac{1}{2}AC•BD=\frac{1}{2}×7×4$=14.
(2)如图2,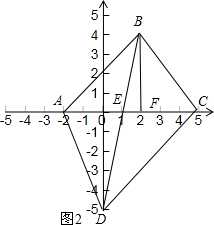
存在D点使得S△ADE=S△BCE
过点C作AB的平行线交y轴负半轴的点即为符合条件的点D
∵AB∥CD
∴S△ADC=S△BDC,等底等高面积相等,
∴S△ADC-S△DCE=S△BDC-S△DCE,
即S△ADE=S△BCE
由A(-2,0),B(2,4),C(5,0)
∴AF=BF=4,∠AFB=90°,
∴△ABF是等腰直角三角形
∴∠BAC=45°
∵AB∥CD,
∴∠ACD=45°
∴△OCD是等腰直角三角形
∴OD=OC=5
∴D(0,-5).
点评 本题考查了坐标与图形,解决本题的关键是正确画出图形,利用数形结合的思想解析解答.

练习册系列答案
相关题目
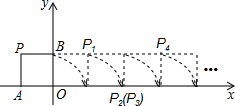 如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2003次,点P依次落在点P1、P2、P3、P4…Pn的位置,则P2003的横坐标x2003=2002.
如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2003次,点P依次落在点P1、P2、P3、P4…Pn的位置,则P2003的横坐标x2003=2002.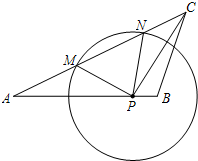 如图,已知在△ABC中,AB=15,AC=20,tanA=$\frac{1}{2}$,点P在AB边上,⊙P的半径为定长.当点P与点B重合时,⊙P恰好与AC边相切;当点P与点B不重合时,⊙P与AC边相交于点M和点N.
如图,已知在△ABC中,AB=15,AC=20,tanA=$\frac{1}{2}$,点P在AB边上,⊙P的半径为定长.当点P与点B重合时,⊙P恰好与AC边相切;当点P与点B不重合时,⊙P与AC边相交于点M和点N.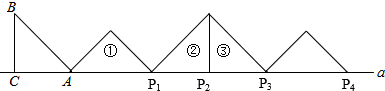
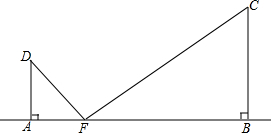 一条宽阔的街道的两侧有两个建筑物AD和BC,王洋在街道的两建筑物之间测AD的仰角为45°,建筑物BC的仰角为57°,已知两建筑物的高度之和为60米,两街道宽AB=50米,求建筑物BC的高度.(sin57°≈0.83,cos57°≈0.54,tan57≈1.5)
一条宽阔的街道的两侧有两个建筑物AD和BC,王洋在街道的两建筑物之间测AD的仰角为45°,建筑物BC的仰角为57°,已知两建筑物的高度之和为60米,两街道宽AB=50米,求建筑物BC的高度.(sin57°≈0.83,cos57°≈0.54,tan57≈1.5) 在猜一商品价格的游戏中,参与者事先不知道该商品的价格,主持人要求他从如图的五张卡片中任意拿走三张,使剩下的卡片从左到右连成一个两位数,该数就是他猜的价格.如果商品的价格是50元,求他一次就能猜中的概率.
在猜一商品价格的游戏中,参与者事先不知道该商品的价格,主持人要求他从如图的五张卡片中任意拿走三张,使剩下的卡片从左到右连成一个两位数,该数就是他猜的价格.如果商品的价格是50元,求他一次就能猜中的概率.