题目内容
11.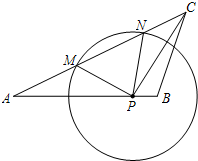 如图,已知在△ABC中,AB=15,AC=20,tanA=$\frac{1}{2}$,点P在AB边上,⊙P的半径为定长.当点P与点B重合时,⊙P恰好与AC边相切;当点P与点B不重合时,⊙P与AC边相交于点M和点N.
如图,已知在△ABC中,AB=15,AC=20,tanA=$\frac{1}{2}$,点P在AB边上,⊙P的半径为定长.当点P与点B重合时,⊙P恰好与AC边相切;当点P与点B不重合时,⊙P与AC边相交于点M和点N.(1)求⊙P的半径;
(2)当AP=$6\sqrt{5}$时,试探究△APM与△PCN是否相似,并说明理由.
分析 (1)作BD⊥AC,垂足为点D.则BD就是⊙P的半径.根据勾股定理即可得出BD,即⊙P的半径;
(2)当AP=6$\sqrt{5}$时,可求出AM、CN.可证出△AMP∽△PNC.
解答 解:(1)作BD⊥AC,垂足为点D.
∵⊙P与边AC相切,
∴BD就是⊙P的半径,
设BD=x,则AD=2x,
由勾股定理得:x2+(2x)2=152,
解得:$x=3\sqrt{5}$,
∴半径为$3\sqrt{5}$;
(2)相似;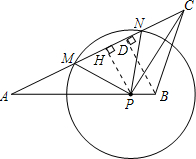
过点P作PH⊥AC于点H,
∵tanA=$\frac{PH}{AH}$=$\frac{1}{2}$,AP=$6\sqrt{5}$,
∴AH=2PH,
∴AH2+PH2=AP2,
即(2PH)2+PH2=(6$\sqrt{5}$)2,
∴PH=6,AH=12,
∵PM=3$\sqrt{5}$,
∴MH=3,
∴AM=9,
∴CN=5,
∴$\frac{AM}{MP}=\frac{PN}{NC}=\frac{3}{{\sqrt{5}}}$,
又∵PM=PN,
∴∠PMN=∠PNM,
∴∠AMP=∠PNC,
∴△AMP∽△PNC.
点评 本题考查了切线的性质,勾股定理相似三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
1.若直线y=-x+a与直线y=x+b的交点坐标为(m,6),则2(a+b)的结果为( )
| A. | 8 | B. | 16 | C. | 24 | D. | 32 |
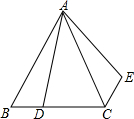 如图,在等边三角形ABC中,AB=6,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为( )
如图,在等边三角形ABC中,AB=6,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为( )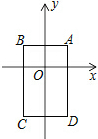 如图,在平面直角坐标系中,已知点A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一根长为2015个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是(-1,-2).
如图,在平面直角坐标系中,已知点A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一根长为2015个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是(-1,-2).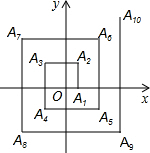 在平面直角坐标系中,点A从原点出发沿x轴正方向移动1个单位到A1,逆时针旋转90°前进2个单位到A2…逆时针旋转90°前进2015个单位到点A2015,则A2015的坐标是(1008,-1006).
在平面直角坐标系中,点A从原点出发沿x轴正方向移动1个单位到A1,逆时针旋转90°前进2个单位到A2…逆时针旋转90°前进2015个单位到点A2015,则A2015的坐标是(1008,-1006).