题目内容
7.对于整数a,b,c,d,定义$|\begin{array}{l}{a}&{b}\\{d}&{c}\end{array}|$=ac-bd,已知1<$|\begin{array}{l}{1}&{b}\\{d}&{4}\end{array}|$<3,则b+d的值为3或-3.分析 根据题意列出不等式,求出b、d的整数解即可解决问题.
解答 解:由题意1<4-bd<3,
∴1<bd<3,
∵b、d都是整数,
∴$\left\{\begin{array}{l}{b=1}\\{d=2}\end{array}\right.$或$\left\{\begin{array}{l}{b=2}\\{d=1}\end{array}\right.$或$\left\{\begin{array}{l}{b=-1}\\{d=-2}\end{array}\right.$或$\left\{\begin{array}{l}{b=-2}\\{d=-1}\end{array}\right.$,
∴b+d=3或-3.
故答案为3或-3.
点评 本题考查不等式、不等式的整数解等整数,解题的关键是理解题意,把问题转化为不等式解决,属于中考常考题型.

练习册系列答案
相关题目
17.湖州师院大学生小王利用暑假开展了30天的社会实践活动,参与了湖州浙北超市的经营,了解到某成本为15元/件的商品在x天销售的相关信息,如表表示:
设该超市在第x天销售这种商品获得的利润为y元.
(1)求y关于x的函数关系式;
(2)在这30天中,该超市销售这种商品第几天的利润最大?最大利润是多少?
| 销售量p(件) | P=45-x |
| 销售单价q(元/件) | 当1≤x≤18时,q=20+x 当18<x≤30时,q=38 |
(1)求y关于x的函数关系式;
(2)在这30天中,该超市销售这种商品第几天的利润最大?最大利润是多少?
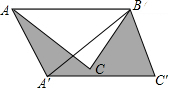 如图,在△ABC中,AB=6cm,∠CAB=45°,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为9$\sqrt{2}$cm2.
如图,在△ABC中,AB=6cm,∠CAB=45°,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为9$\sqrt{2}$cm2. 己知:直线y=x+3与x轴、y轴分别交于点A、B,抛物线y=ax2+bx+c(a、b、c均不为0)与x轴交于点C、D两点.
己知:直线y=x+3与x轴、y轴分别交于点A、B,抛物线y=ax2+bx+c(a、b、c均不为0)与x轴交于点C、D两点. 如图,一货船在港口A的正北100 n mi1e的B处,遇到危险后,以25 n mile/h的速度向正东漂行且发出求救信号,一军舰接到求救信号后立即由港口A以50 n mile/h的速度向北偏东方向航行,赶去支援,求军舰航行$\frac{200\sqrt{3}}{3}$n mi1e可追上货船.
如图,一货船在港口A的正北100 n mi1e的B处,遇到危险后,以25 n mile/h的速度向正东漂行且发出求救信号,一军舰接到求救信号后立即由港口A以50 n mile/h的速度向北偏东方向航行,赶去支援,求军舰航行$\frac{200\sqrt{3}}{3}$n mi1e可追上货船.
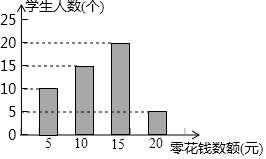 某教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行统计调查,并绘制了统计表及统计图,如图所示.
某教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行统计调查,并绘制了统计表及统计图,如图所示.