题目内容
17.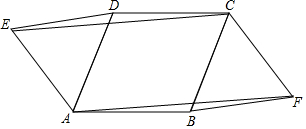 如图,以?ABCD的边AD、BC为边向外作等边三角形ADE和BCF,连接CE、AF,求证:四边形AECF是平行四边形.
如图,以?ABCD的边AD、BC为边向外作等边三角形ADE和BCF,连接CE、AF,求证:四边形AECF是平行四边形.
分析 只要证明△ABF≌△CDE,可得AF=EC再证明AE=CF即可解决问题.
解答  证明:∵四边形ABCD是平行四边形,
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠ABC=∠ADC,
∵△ADE,△BCF都是等边三角形,
∴AD=DE=AE,BC=BF=CF,∠ADE=∠CBF=60°,
∴∠ABF=∠EDC,DE=BF.AE=CF,
在△ABF和△CDE中,
$\left\{\begin{array}{l}{AB=CD}\\{∠ABF=∠EDC}\\{DE=BF}\end{array}\right.$.
∴△ABF≌△CDE.
∴AF=EC,∵AE=CF,
∴四边形AECF是平行四边形.
点评 本题考查平行四边形的性质和判定、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题.

练习册系列答案
相关题目
12.某校运动员进行分组训练,若每组5人,余2人,若每组6人,则缺3人,设运动员人数为x人,组数为y,则根据题意所列方程组为( )
| A. | $\left\{\begin{array}{l}{5y=x+2}\\{6x+3=x}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{5y=x+2}\\{6y-3=x}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{5y=x-2}\\{6y=x+3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{5y=x-2}\\{6y=x-3}\end{array}\right.$ |
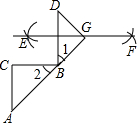 如图,在△ABC中,∠C=90°,DB⊥BC于点B,分别以点D和点B为圆心,以大于$\frac{1}{2}$DB的长为半径作弧,两弧相交于点E和点F,作直线EF,延长AB于点G,连接DG,下面是说明∠A=∠D的说理过程,请把下面的说理过程补充完整:
如图,在△ABC中,∠C=90°,DB⊥BC于点B,分别以点D和点B为圆心,以大于$\frac{1}{2}$DB的长为半径作弧,两弧相交于点E和点F,作直线EF,延长AB于点G,连接DG,下面是说明∠A=∠D的说理过程,请把下面的说理过程补充完整: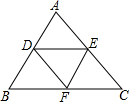 如图,已知点D,E,F分别在 AB,AC,BC边上,且DE∥BC,DF∥AC,∠B=60°,∠C=50°.
如图,已知点D,E,F分别在 AB,AC,BC边上,且DE∥BC,DF∥AC,∠B=60°,∠C=50°.