题目内容
解不等式|2x2-5|＞3x．
考点：一元二次不等式
专题：
分析：分类讨论当2x2-5≥0时，原不等式可变形为2x2-5＞3x，当2x2-5＜0时，原不等式可变形为-2x2+5＞3x，再分别求解即可．
解答：解：当2x2-5≥0时，原不等式可变形为2x2-5＞3x，解得：x＜-1或x＞
，
当2x2-5＜0时，原不等式可变形为-2x2+5＞3x，解得：-
＜x＜1．
则当2x2-5≥0时，x＜-1或x＞
，
当2x2-5＜0时，-
＜x＜1．
| 5 |
| 2 |
当2x2-5＜0时，原不等式可变形为-2x2+5＞3x，解得：-
| 5 |
| 2 |
则当2x2-5≥0时，x＜-1或x＞
| 5 |
| 2 |
当2x2-5＜0时，-
| 5 |
| 2 |
点评：本题考查了一元二次不等式，用到的知识点是二次函数与不等式及绝对值，难度适中，关键是注意分类讨论去掉绝对值符号．
练习册系列答案
相关题目
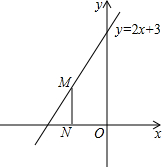如图，点M是直线y=2x+3上的动点，过点M作MN垂直于x轴于点N，y轴上是否存在点P，使△MNP为等腰直角三角形．小明发现：当动点M运动到（-1，1）时，y轴上存在点P（0，1），此时有MN=MP，能使△NMP为等腰直角三角形．那么，在y轴和直线上是否还存在符合条件的点P和点M呢？请你写出其它符合条件的点P的坐标．