题目内容
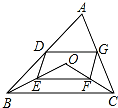 点O是三角形ABC所在平面内一动点,连接OB、OC,并将AB、OB、OC、AC中点D、E、F、G,依次连接起来,设DEFG能构成四边形.
点O是三角形ABC所在平面内一动点,连接OB、OC,并将AB、OB、OC、AC中点D、E、F、G,依次连接起来,设DEFG能构成四边形.(1)如图,当点O在△ABC内时,求证:四边形DEFG是平行四边形;
(2)若四边形DEFG是正方形,则线段AO与BC应满足条件
考点:三角形中位线定理,平行四边形的判定,正方形的性质
专题:
分析:(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得DG∥BC,DG=
BC,EF∥BC,EF=
BC,从而得到DG∥EF,DG=EF,然后根据一组对边平行且相等的四边形是平行四边形证明即可;
(2)根据三角形的中位线平行于第三边并且等于第三边的一半可得DE∥OA,DE=
OA,再根据邻边垂直相等的平行四边形是正方形解答.
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据三角形的中位线平行于第三边并且等于第三边的一半可得DE∥OA,DE=
| 1 |
| 2 |
解答:(1)证明:∵AB、OB、OC、AC的中点分别为D、E、F、G,
∴DG∥BC,DG=
BC,EF∥BC,EF=
BC,
∴DG∥EF,DG=EF,
∴四边形DEFG是平行四边形;
(2)解:∵D、E分别是AB、OB的中点,
∴DE∥OA,DE=
OA,
∵四边形DEFG是正方形,
∴DE⊥EF,DE=EF,
∴AO与BC垂直且相等.
故答案为:垂直且相等.
∴DG∥BC,DG=
| 1 |
| 2 |
| 1 |
| 2 |
∴DG∥EF,DG=EF,
∴四边形DEFG是平行四边形;
(2)解:∵D、E分别是AB、OB的中点,
∴DE∥OA,DE=
| 1 |
| 2 |
∵四边形DEFG是正方形,
∴DE⊥EF,DE=EF,
∴AO与BC垂直且相等.
故答案为:垂直且相等.
点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,平行四边形的判定,正方形的判定,熟记定理是解题的关键,(2)理解正方形与平行四边形的关系是解题的关键.

练习册系列答案
相关题目
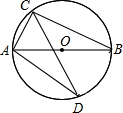 如图,点C为圆上一点,⊙O直径AB为10cm,∠ACB的平分线交⊙O于D.
如图,点C为圆上一点,⊙O直径AB为10cm,∠ACB的平分线交⊙O于D. 如图,点C为线段AB上任意一点(不与点A、B重合),分别以AC、BC为一腰在AB的同侧作等腰三角形ACD和等腰三角形BCE,CA=CD,CB=CE,∠ACD与∠BCE都是锐角,且∠ACD=∠BCE,连接AE交CD于点M,连接BD交CE于点N,AE与BD相交于点P,连接PC.求证:
如图,点C为线段AB上任意一点(不与点A、B重合),分别以AC、BC为一腰在AB的同侧作等腰三角形ACD和等腰三角形BCE,CA=CD,CB=CE,∠ACD与∠BCE都是锐角,且∠ACD=∠BCE,连接AE交CD于点M,连接BD交CE于点N,AE与BD相交于点P,连接PC.求证: