题目内容
1.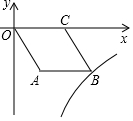 如图,O是坐标原点,菱形OABC的顶点A的坐标为(6,-8),顶点C在x轴的正半轴上,若函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )
如图,O是坐标原点,菱形OABC的顶点A的坐标为(6,-8),顶点C在x轴的正半轴上,若函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )| A. | -48 | B. | -64 | C. | -96 | D. | -128 |
分析 根据菱形的性质以及勾股定理得出AO=AB=10,即可得出B点坐标,进而求出k的值.
解答 解:∵菱形OABC的顶点C在x轴的正半轴上,顶点A的坐标为(6,-8),
∴AO=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴AO=AB=10,
∴B(16,-8),
∴k=xy=16×(-8)=-128.
故选;D.
点评 此题主要考查了菱形的性质以及勾股定理和反比例函数图象上点的坐标性质,得出B点坐标是解题关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
12.将抛物线y=x2向右平移1个单位长度,再向上平移2个单位长度所得的抛物线解析式为( )
| A. | y=(x-1)2+2 | B. | y=(x+1)2+2 | C. | y=(x-1)2-2 | D. | y=(x+1)2-2 |
9.一元二次方程x2=x的根是( )
| A. | x=1 | B. | x=0 | C. | x1=0,x2=1 | D. | 非以上答案 |
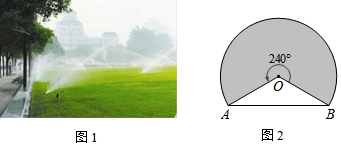
16.如图(1)是某公园一块草坪上的自动旋转喷水装置,这种旋转喷水装置的旋转角度为240°,它的喷灌区是如图(2)所示的扇形.如果A,B两点的距离为18m,那么这种装置能够喷灌的草坪面积为72πm2.

13.(-2)2的算术平方根是( )
| A. | -2 | B. | ±2 | C. | 2 | D. | $\sqrt{2}$ |
 在如图所示的运算流程中,若输入的数x=-4,则输出的数y=-8.
在如图所示的运算流程中,若输入的数x=-4,则输出的数y=-8.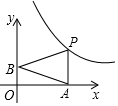 如图,已知动点A,B分别在x轴,y轴正半轴上,动点P在反比例函数y=$\frac{6}{x}$(x>0)图象上,PA⊥x轴,△PAB是以PA为底边的等腰三角形.当点A的横坐标逐渐增大时,△PAB的面积将会( )
如图,已知动点A,B分别在x轴,y轴正半轴上,动点P在反比例函数y=$\frac{6}{x}$(x>0)图象上,PA⊥x轴,△PAB是以PA为底边的等腰三角形.当点A的横坐标逐渐增大时,△PAB的面积将会( )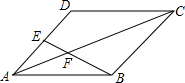 如图,在?ABCD中,点E为AD的中点,连接BE,交AC于点F.
如图,在?ABCD中,点E为AD的中点,连接BE,交AC于点F.