题目内容
已知二次函数y=a(x+1)(x-3)的图象与x轴交于点A,B,与y轴交于点C,则使△ABC为等腰三角形的a的值为 .
考点:抛物线与x轴的交点
专题:
分析:由y=a(x+1)(x-3)求出A、B、C三点坐标,再分情况讨论:①AC=BC;②AB=AC;③AB=BC分别满足时a的取值.
解答:解:由y=a(x+1)(x-3),则可得出A(-1,0)、B( 3,0);
再令x=0,y=-3a,则可得出C点坐标为(0,-3a).
由于△ABC是等腰三角形,则分以下三种情况讨论:
(1)若AC=BC,由于OA≠OB,∴这种情况不存在.
(2)若AB=AC,则AC2=OA2+OC2,
∴42=12+(-3a)2,
解得:a=
或-
.
(3)若AB=BC,则BC2=OB2+OC2,
∴42=32+(-3a)2,
解得:a=
或-
.
故答案为
或-
或
或-
.
再令x=0,y=-3a,则可得出C点坐标为(0,-3a).
由于△ABC是等腰三角形,则分以下三种情况讨论:
(1)若AC=BC,由于OA≠OB,∴这种情况不存在.
(2)若AB=AC,则AC2=OA2+OC2,
∴42=12+(-3a)2,
解得:a=
| ||
| 3 |
| ||
| 3 |
(3)若AB=BC,则BC2=OB2+OC2,
∴42=32+(-3a)2,
解得:a=
| ||
| 3 |
| ||
| 3 |
故答案为
| 1 |
| 3 |
| 7 |
| 1 |
| 3 |
| 7 |
| 1 |
| 3 |
| 15 |
| 1 |
| 3 |
| 15 |
点评:本题考查了数形结合的思想,由等腰三角形的两腰相等确定点的坐标,再求解析式里的未知量.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1-(x-a)(x-b)=0的两根,且a<b,则a、b、m、n的大小关系是( )
| A、m<a<b<n |
| B、a<m<n<b |
| C、a<m<b<n |
| D、m<a<n<b |
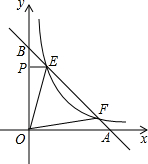 如图,点E,F在函数y=
如图,点E,F在函数y= 如图,C为⊙O外一点,CA与⊙O相切,切点为A,AB为⊙O的直径,连接CB.若⊙O的半径为2,∠ABC=60°,则BC=
如图,C为⊙O外一点,CA与⊙O相切,切点为A,AB为⊙O的直径,连接CB.若⊙O的半径为2,∠ABC=60°,则BC=