题目内容
16.用适当的方法解下列方程(1)2y2-4y=4
(2)x2+3=2$\sqrt{3}$x
(3)(x-2)(x+3)=-6
(4)3x(x-2)=2(2-x)
(5)3x2-2=4x.
分析 (1)利用配方法求解即可.
(2)利用因式分解法求解即可.
(3)整理后利用因式分解法解.
(4)利用提公因式法求解即可.
(5)化为一般式利用公式法求解即可.
解答 解:(1)整理得到y2-2y-2=0,
∴y2-2y+1=3,
∴(y-1)2=3,
∴y-1=$±\sqrt{3}$,
∴y1=1+$\sqrt{3}$,y2=1-$\sqrt{3}$.
(2)∵x2+3=2$\sqrt{3}$x,
∴(x-$\sqrt{3}$)2=0,
∴x1=x2=$\sqrt{3}$.
(3)整理得到x2+x=0,
∴x(x+1)=0,
∴x1=0,x2=-1.
(4)∵3x(x-2)=2(2-x),
∴(x-2)(3x+2)=0,
∴x1=2,x2=-$\frac{2}{3}$,
(5)∵3x2-2=4x,
∴3x2-4x-2=0,
∴a=3,b=-4,c=-2,
∴△=40>0,
∴x=$\frac{4±2\sqrt{10}}{6}$,
∴x1=$\frac{2+\sqrt{10}}{3}$,x2=$\frac{2-\sqrt{10}}{3}$.
点评 本题考查一元二次方程的解法,解题的关键是灵活掌握一元二次方程的解法,一元二次方程的解法有直接开方法,因式分解法,公式法,配方法,属于中考常考题型.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
7.下列各题去括号所得结果正确的是( )
| A. | x2-(x-y+2z)=x2-x+y+2z | B. | x-[-y+(-3x+1)]=x+y+3x-1 | ||
| C. | 3x-[5x-(x-1)]=3x-5x-x+1 | D. | (x-1)-(x2-2)=x-1-x2-2 |
8.下列运算正确的是( )
| A. | x2+x3=x5 | B. | x4•x2=x6 | C. | (x2)3=x8 | D. | x6÷x2=x3 |
6.下列二次根式中,与$\sqrt{8}$是同类二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
 已知:如图,平行四边形ACBD中,对角线AC、BD相交于点O,延长CD至F,使DF=CD,连接BF交AD于点E.
已知:如图,平行四边形ACBD中,对角线AC、BD相交于点O,延长CD至F,使DF=CD,连接BF交AD于点E.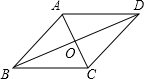 如图,四边形ABCD的对角线互相平分,若再补充一个条件能使四边形ABCD成为矩形,则这个条件是AC=BD(答案不唯一)(只填一个条件即可)
如图,四边形ABCD的对角线互相平分,若再补充一个条件能使四边形ABCD成为矩形,则这个条件是AC=BD(答案不唯一)(只填一个条件即可) 已知:如图,BC∥AD,∠A=∠B.
已知:如图,BC∥AD,∠A=∠B.