Question

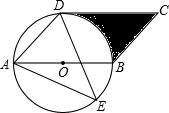如图，四边形ABCD是平行四边形，以AB为直径的⊙O经过点D，E是⊙O上一点，若⊙O的半径为6cm，且∠AED=45°．
（1）判断CD与⊙O的位置关系，并说明理由
（2）求图中阴影部分面积；
（3）若sin∠ADE=

3

2

，求线段DE的长．

Answer 1

考点：切线的判定,扇形面积的计算

专题：计算题

分析：（1）连接OD、DB，根据圆周角定理得到∠ADB=90°，∠ABD=∠AED=45°，则△ADB为等腰直角三角形，所以DO⊥AB，再根据平行四边形的性质得DC∥AB，所以DO⊥DC，于是可根据切线的判定定理得到DC为⊙O的切线；
（2）根据平行四边形的性质得DC=AB=12cm，然后根据扇形的面积公式和阴影部分面积=S_梯形DOBC-S_扇形BOD进行计算；
（3）作AH⊥DE于H，由△ADB为等腰直角三角形得到AD=

2

2

AB=6

2

，再根据特殊角的三角函数值得到∠ADH=60°，然后根据含30度的直角三角形三边的关系得到DH=

1

2

AD=3

2

，AH=

3

DH=3

6

，在Rt△AEH中，根据等腰直角三角形的性质得EH=AH=3

6

，所以DE=（3

2

+3

6

）cm．

解答：解：（1）CD与⊙O相切．理由如下：
连接OD、DB，如图，
∵AB⊙O的直径，
∴∠ADB=90°，
∵∠ABD=∠AED=45°，
∴△ADB为等腰直角三角形，
∴DO⊥AB，
∵四边形ABCD是平行四边形，
∴DC∥AB，
∴DO⊥DC，
∴DC为⊙O的切线；
（2）∵四边形ABCD是平行四边形，
∴DC=AB=12cm，
∴阴影部分面积=S_梯形DOBC-S_扇形BOD
=

1

2

×（6+12）×6-

90•π•62

360

=（54-9π）cm²；
（3）作AH⊥DE于H，如图，
∵△ADB为等腰直角三角形，
∴AD=

2

2

AB=6

2

，
∵sin∠ADE=

3

2

，
∴∠ADH=60°，
在Rt△ADH中，DH=

1

2

AD=3

2

，
AH=

3

DH=3

6

，
在Rt△AEH中，EH=AH=3

6

，
∴DE=（3

2

+3

6

）cm．

点评：本题考查了切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．也考查了平行四边形的性质和扇形的面积公式．