题目内容
7.如图,在矩形纸片ABCD中,已知AB=1,BC=$\sqrt{3}$,点E在边CD上移动,连接AE,将多边形ABCE沿直线AE翻折,得到多边形AB′C′E,点B、C的对应点分别为点B′、C′.(1)当B′C′恰好经过点D时(如图1),求线段CE的长;
(2)若B′C′分别交边AD,CD于点F,G,且∠DAE=22.5°(如图2),求△DFG的面积;
(3)在点E从点C移动到点D的过程中,求点C′运动的路径长.

分析 (1)如图1中,设CE=EC′=x,则DE=1-x,由△ADB′′∽△DEC,可得$\frac{AD}{DE}$=$\frac{DB′}{EC′}$,列出方程即可解决问题;
(2)如图2中,首先证明△ADB′,△DFG都是等腰直角三角形,求出DF即可解决问题;
(3)如图3中,点C的运动路径的长为$\widehat{CC′}$的长,求出圆心角、半径即可解决问题.
解答 解:(1)如图1中,设CE=EC′=x,则DE=1-x,
∵∠ADB′+∠EDC′=90°,∠B′AD+∠ADB′=90°,
∴∠B′AD=∠EDC′,
∵∠B′=∠C′=90°,AB′=AB=1,AD=$\sqrt{3}$,
∴DB′=$\sqrt{3-1}$=$\sqrt{2}$,
∴△ADB′∽△DEC′,
∴$\frac{AD}{DE}$=$\frac{DB′}{EC′}$,
∴$\frac{\sqrt{3}}{1-x}$=$\frac{\sqrt{2}}{x}$,
∴x=$\sqrt{6}$-2.
∴CE=$\sqrt{6}$-2.
(2)如图2中,
∵∠BAD=∠B′=∠D=90°,∠DAE=22.5°,
∴∠EAB=∠EAB′=67.5°,
∴∠B′AF=∠B′FA=45°,
∴∠DFG=∠AFB′=∠DGF=45°,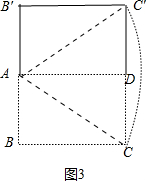
∴DF=DG,
在Rt△AB′F中,AB′=FB′=1,
∴AF=$\sqrt{2}$AB′=$\sqrt{2}$,
∴DF=DG=$\sqrt{3}$-$\sqrt{2}$,
∴S△DFG=$\frac{1}{2}$($\sqrt{3}$-$\sqrt{2}$)2=$\frac{5}{2}$-$\sqrt{6}$.
(3)如图3中,点C的运动路径的长为$\widehat{CC′}$的长,
在Rt△ADC中,∵tan∠DAC=$\frac{CD}{AD}$=$\frac{\sqrt{3}}{3}$,
∴∠DAC=30°,AC=2CD=2,
∵∠C′AD=∠DAC=30°,
∴∠CAC′=60°,
∴$\widehat{CC′}$的长=$\frac{60•π•2}{180}$=$\frac{2}{3}$π.
点评 本题考查四边形综合题、矩形的性质、相似三角形的判定和性质、勾股定理、弧长公式等知识,解题的关键是正确寻找相似三角形解决问题,学会用构建方程的思想思考问题.属于中考压轴题.

| A. | x<1 | B. | x≥1 | C. | x≤-1 | D. | x<-1 |
| A. | 没有实数根 | B. | 只有一个实数根 | ||
| C. | 两个相等的实数根 | D. | 两个不相等的实数根 |
| A. | 12 | B. | 27 | C. | 36 | D. | 45 |
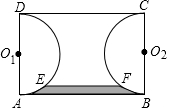 如图,已知矩形ABCD中,AB=3,AD=2,分别以边AD,BC为直径在矩形ABCD的内部作半圆O1和半圆O2,一平行于AB的直线EF与这两个半圆分别交于点E、点F,且EF=2(EF与AB在圆心O1和O2的同侧),则由$\widehat{AE}$,EF,$\widehat{FB}$,AB所围成图形(图中阴影部分)的面积等于3-$\frac{5\sqrt{3}}{4}$-$\frac{π}{6}$.
如图,已知矩形ABCD中,AB=3,AD=2,分别以边AD,BC为直径在矩形ABCD的内部作半圆O1和半圆O2,一平行于AB的直线EF与这两个半圆分别交于点E、点F,且EF=2(EF与AB在圆心O1和O2的同侧),则由$\widehat{AE}$,EF,$\widehat{FB}$,AB所围成图形(图中阴影部分)的面积等于3-$\frac{5\sqrt{3}}{4}$-$\frac{π}{6}$.