题目内容
17.在平面直角坐标系xOy中有一矩形ABCD,如果A(1,0)、B(5,0)、C(5,3),那么该矩形对角线交点P的坐标为(3,1.5).分析 由矩形的性质得出AP=CP,利用中点坐标公式即可求出P点坐标,
解答 解:(1)∵四边形ABCD是矩形,
∴AP=CP,
∵点A (1,0),C(5,3),
∴对角线的交点P($\frac{1+5}{2}$,$\frac{0+3}{2}$),
即(3,1.5),
故答案为:(3,1.5).
点评 本题主要考查了矩形的性质、坐标与图形性质、中点坐标公式;熟记矩形的性质和公式是关键

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列运算中,正确的是( )
| A. | x2+x3=x5 | B. | (x3)4=x7 | C. | x6÷x2=x3 | D. | 3x2-x2=2x2 |
2.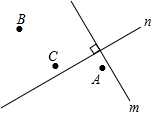 如图,直线m⊥n,在某平面直角坐标系中,x轴∥m,y轴∥n,点A的坐标为(4,2),点B的坐标为(-2,-2),则点C的坐标为( )
如图,直线m⊥n,在某平面直角坐标系中,x轴∥m,y轴∥n,点A的坐标为(4,2),点B的坐标为(-2,-2),则点C的坐标为( )
 如图,直线m⊥n,在某平面直角坐标系中,x轴∥m,y轴∥n,点A的坐标为(4,2),点B的坐标为(-2,-2),则点C的坐标为( )
如图,直线m⊥n,在某平面直角坐标系中,x轴∥m,y轴∥n,点A的坐标为(4,2),点B的坐标为(-2,-2),则点C的坐标为( )| A. | (2,1) | B. | (-2,1) | C. | (2,-1) | D. | (-2,-1) |
9.能与60°的角互余的角是( )
| A. |  | B. |  | C. |  | D. |  |
6.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |

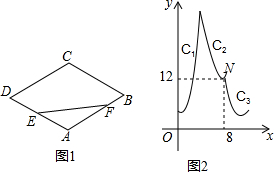 如图1,在菱形ABCD中,点E为AD的中点,点F为折线A-B-C-D上一个动点(从点A出发到点D停止),连结EF,设点F的运动路径的长为x,EF2为y,y关于x的函数图象由C1,C2,C3三段组成,已知C2与C3的界点N的坐标如图2所示.
如图1,在菱形ABCD中,点E为AD的中点,点F为折线A-B-C-D上一个动点(从点A出发到点D停止),连结EF,设点F的运动路径的长为x,EF2为y,y关于x的函数图象由C1,C2,C3三段组成,已知C2与C3的界点N的坐标如图2所示.
