题目内容
13. 如图,直线l1∥l2,∠1=35°,∠2=75°,则∠3等于( )
如图,直线l1∥l2,∠1=35°,∠2=75°,则∠3等于( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
分析 根据两直线平行,内错角相等可得∠4=∠2,再根据三角形的内角和定理列式计算即可得解.
解答  解:∵l1∥l2,
解:∵l1∥l2,
∴∠4=∠2=75°,
∴∠3=180°-∠1-∠4=180°-35°-75°=70°.
故选D.
点评 本题考查了平行线的性质,三角形的内角和定理,熟记性质并准确识图是解题的关键.

练习册系列答案
相关题目
3.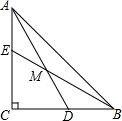 如图,△ABC中,AC=BC,∠ACB=90°,D,E分别是BC,AC上一点,BD=AE,BE,AD交于M,
如图,△ABC中,AC=BC,∠ACB=90°,D,E分别是BC,AC上一点,BD=AE,BE,AD交于M,
(1)求证:AM=BM;
(2)若∠BMD=45°,求$\frac{BM}{EM}$的值.
 如图,△ABC中,AC=BC,∠ACB=90°,D,E分别是BC,AC上一点,BD=AE,BE,AD交于M,
如图,△ABC中,AC=BC,∠ACB=90°,D,E分别是BC,AC上一点,BD=AE,BE,AD交于M,(1)求证:AM=BM;
(2)若∠BMD=45°,求$\frac{BM}{EM}$的值.
1.下列四种标志图案中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
8.下列四个数-2,0,0.5,$\sqrt{2}$中,属于无理数的是( )
| A. | -2 | B. | 0 | C. | 0.5 | D. | $\sqrt{2}$ |
3.下列计算正确的是( )
| A. | -3-3=0 | B. | 20+32=9 | C. | 3÷|-3|=-1 | D. | 3×(-3)-1=-1 |
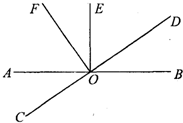 如图,直线AB与CD相交于点D,OE⊥AB,OF⊥CD.
如图,直线AB与CD相交于点D,OE⊥AB,OF⊥CD.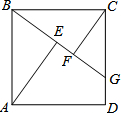 如图,在正方形ABCD中,点G是CD上任意一点,连接BG,作AE⊥BG于点E,CF⊥BG于点F.
如图,在正方形ABCD中,点G是CD上任意一点,连接BG,作AE⊥BG于点E,CF⊥BG于点F.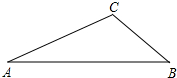 已知△ABC中,∠A=25°,∠B=40°.
已知△ABC中,∠A=25°,∠B=40°.