题目内容
12.如图(a),抛物线y1=a(x-2)2-1的顶点为M,交x轴于A,B两点,交y轴于C点,且OA+OB=OC+1.(1)求该抛物线的解析式.
(2)如图(b),P为M点右侧抛物线图象上一点,CH⊥PM于H,若CA=CH,求P点坐标.
(3)将原抛物线绕平面内某一点旋转180°,得到新的抛物线y2,其顶点为E,设D为原抛物线y1对称轴上一点,当四边形BCDE为菱形时(按字母顺序构图),求y2的解析式.
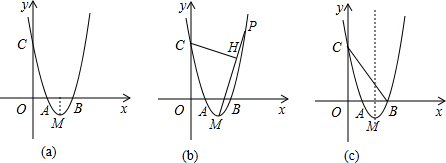
分析 (1)令y1=0,根据根与系数关系,得OA=OB=4,得OC=3,列出方程求出a即可解决问题.
(2)如图(b)中,过点H作EF∥y轴,CE⊥EF于E,MF⊥EF于F,连接MC,AC.由△CEH∽△HFM,得$\frac{CH}{MH}$=$\frac{EC}{HF}$=$\frac{EH}{MF}$,在Rt△CMH中求出HM,推出CH=MH,CE=HF,EH=FM,设MF=a,则EH=a,CE=HF=2+a,由EH+HF=4,列出方程即可解决问题.
(3)分两种情形讨论①当点D在BC上方时,②当点D在BC下方时,先求出D点坐标,设E(m,n),利用中点坐标公式列出方程组即可解决问题.
解答 解:(1)∵y1=a(x-2)2-1=ax2-4ax+4a-1,
令y1=0,则有ax2-2ax+4a-1=0,
∴OA+OB=4,
∵OA+OB=OC+1,
∴OC=3,
∴4a-3=1,
∴a=1,
∴抛物线解析式为y=(x-2)2-1,即y=x2-4x+3.
(2)如图(b)中,过点H作EF∥y轴,CE⊥EF于E,MF⊥EF于F,连接MC,AC.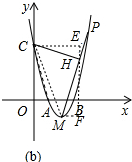
∵CH⊥PM,
∴∠CHM=∠CEH=∠MFH=90°,
∴∠CHE+∠HCE=90°,∠CHE+∠MHF=90°,
∴∠HCE=∠MHF,
∴△CEH∽△HFM,
∴$\frac{CH}{MH}$=$\frac{EC}{HF}$=$\frac{EH}{MF}$,
∵A(1,0),C(0,3),
∴OA=1,OC=3,AC=$\sqrt{10}$,MC=2$\sqrt{5}$,
∵AC=CH,
∴HM=$\sqrt{C{M}^{2}-C{H}^{2}}$=$\sqrt{20-10}$=$\sqrt{10}$,
∴CH=HH,EC=HF,EH=MF,设MF=a,则EH=a,CE=HF=2+a,
由EH+HF=4,得a+2+a=4,
∴a=1,
∴点H坐标(3,2),
设直线MH的解析式为y=kx+b,则有$\left\{\begin{array}{l}{3k+b=2}\\{2k+b=-1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=3}\\{b=-7}\end{array}\right.$,
∴直线MH的解析式为y=3x-7,
由$\left\{\begin{array}{l}{y=3x-7}\\{y={x}^{2}-4x+3}\end{array}\right.$解得$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$或$\left\{\begin{array}{l}{x=5}\\{y=8}\end{array}\right.$,
∴点P坐标为(5,8).
(3)如图(c)中,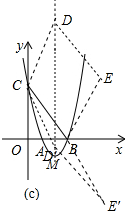
①当点D在BC上方时,∵四边形BCDE是菱形,
∴BC=CD=3$\sqrt{2}$,
∴点D坐标(2,3+$\sqrt{14}$),设E(m,n),
则有$\left\{\begin{array}{l}{\frac{2+3}{2}=\frac{0+m}{2}}\\{\frac{3+\sqrt{14}}{2}=\frac{3+n}{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=5}\\{n=\sqrt{14}}\end{array}\right.$,
∴点E坐标(5,$\sqrt{14}$),
∴新的抛物线y2的解析式为y2=-(x-5)2+$\sqrt{14}$.
②当点D在BC下方时,∵四边形BCD′E′是菱形,
∴BC=CD′=3$\sqrt{2}$,
∴点D′坐标(2,3-$\sqrt{14}$),设E′(m,n),
则有$\left\{\begin{array}{l}{\frac{2+3}{2}=\frac{0+m}{2}}\\{\frac{0+3-\sqrt{14}}{2}=\frac{3+n}{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=5}\\{n=-\sqrt{14}}\end{array}\right.$,
∴点E坐标(5,-$\sqrt{14}$),
∴新的抛物线y2的解析式为y2=-(x-5)2-$\sqrt{14}$.
综上所述,新的抛物线y2的解析式为y2=-(x-5)2+$\sqrt{14}$或y2=-(x-5)2-$\sqrt{14}$.
点评 本题考查二次函数综合题、一次函数、相似三角形的判定和性质、勾股定理、中点坐标公式等知识,解题的关键是学会构建一次函数,利用方程组求交点坐标,学会利用参数转化为方程组解决问题,属于中考压轴题.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{2-x}{1-x}$ | B. | x+1 | C. | x-1 | D. | $\frac{1}{2-x}$ |
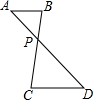 如图,AB∥CD,AD与BC相交于点P,AB=3,CD=6,AP=4,则DP的长为( )
如图,AB∥CD,AD与BC相交于点P,AB=3,CD=6,AP=4,则DP的长为( )| A. | 3 | B. | 4 | C. | 6 | D. | 8 |
 如图,一棵大树在一次强台风中距地面5m处折断,倒下后树顶端着地点A距树底端B的距离为12m,这棵大树在折断前的高度为( )
如图,一棵大树在一次强台风中距地面5m处折断,倒下后树顶端着地点A距树底端B的距离为12m,这棵大树在折断前的高度为( )| A. | 10 m | B. | 15 m | C. | 18 m | D. | 20 m |