题目内容
3.已知a1=x-1(x≠1且x≠2),a2=$\frac{1}{1-{a}_{1}}$,a3=$\frac{1}{1-{a}_{2}}$,…,an=$\frac{1}{1-{a}_{n-1}}$,则a2016等于( )| A. | $\frac{2-x}{1-x}$ | B. | x+1 | C. | x-1 | D. | $\frac{1}{2-x}$ |
分析 把a1代入确定出a2,把a2代入确定出a3,依此类推,得到一般性规律,即可确定出a2016的值.
解答 解:∵a1=x-1(x≠1且x≠2),
∴a2=$\frac{1}{1-{a}_{1}}$=$\frac{1}{1-x+1}$=$\frac{1}{2-x}$,
a3=$\frac{1}{1-{a}_{2}}$=$\frac{1}{1-\frac{1}{2-x}}$=$\frac{2-x}{1-x}$,
a4=$\frac{1}{1-{a}_{3}}$=$\frac{1}{1-\frac{2-x}{1-x}}$=x-1…,
∴三个数一循环,
∵2016÷3=672,
∴a2016=$\frac{2-x}{1-x}$;
故选A.
点评 此题考查了数字的变化类,用到的知识点是分式的混合运算,弄清题中的规律是解本题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
13.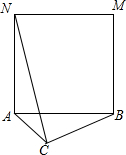 如图,已知△ABC中,AC=2,BC=4,以AB为边向形外作正方形ABMN,若∠ACB的度数发生变化,连接CN,则CN的最大值是( )
如图,已知△ABC中,AC=2,BC=4,以AB为边向形外作正方形ABMN,若∠ACB的度数发生变化,连接CN,则CN的最大值是( )
 如图,已知△ABC中,AC=2,BC=4,以AB为边向形外作正方形ABMN,若∠ACB的度数发生变化,连接CN,则CN的最大值是( )
如图,已知△ABC中,AC=2,BC=4,以AB为边向形外作正方形ABMN,若∠ACB的度数发生变化,连接CN,则CN的最大值是( )| A. | 4$\sqrt{2}$ | B. | 6$\sqrt{2}$ | C. | 4+2$\sqrt{2}$ | D. | 2+4$\sqrt{2}$ |
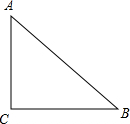 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,现有一点O从点A出发,沿AB方向运动,当到达点B时,运动停止,以点O为圆心,r为半径的圆记为⊙O.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,现有一点O从点A出发,沿AB方向运动,当到达点B时,运动停止,以点O为圆心,r为半径的圆记为⊙O.
 如图是由边长为2的六个等边三角形组成的正六边形,建立适当的直角坐标系,求各顶点的坐标.
如图是由边长为2的六个等边三角形组成的正六边形,建立适当的直角坐标系,求各顶点的坐标.