题目内容

17．如图，一棵大树在一次强台风中距地面5m处折断，倒下后树顶端着地点A距树底端B的距离为12m，这棵大树在折断前的高度为（　　）
A．10 mB．15 mC．18 mD．20 m

分析 根据大树的折断部分与未断部分、地面恰好构成直角三角形，再根据勾股定理求出AC的长，进而可得出结论．

解答 解：∵树的折断部分与未断部分、地面恰好构成直角三角形，且BC=5m，AB=12m，
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{1{2}^{2}+{5}^{2}}$=13m，
∴这棵树原来的高度=BC+AC=5+13=18m．
答：棵树原来高18m．

点评 本题考查的是勾股定理的应用，熟知直角三角形斜边的平方等于两直角边的平方和是解答此题的关键．

练习册系列答案
相关题目
10．如果10m=a，10n=b，求
（1）102m+10n
（2）102m+n的值（m、n为整数）．
8．定义一个新运算如下：
$1?2=-\frac{3}{2}$，$2?1=\frac{3}{2}$，$2?5=-\frac{21}{10}$，$5?（-2）=\frac{21}{10}$，…，
试写出a?b=$\frac{{a}^{2}{-b}^{2}}{|ab|}$．
5．如图，在△ABC中，已知∠ABC=90°，在AB上取一点E，以BE为直径的☉O恰与AC相切于点D．若AE=2，AD=4．则☉O的直径BE=6；△ABC的面积为24．
12．如图（a），抛物线y1=a（x-2）2-1的顶点为M，交x轴于A，B两点，交y轴于C点，且OA+OB=OC+1．
（1）求该抛物线的解析式．
（2）如图（b），P为M点右侧抛物线图象上一点，CH⊥PM于H，若CA=CH，求P点坐标．
（3）将原抛物线绕平面内某一点旋转180°，得到新的抛物线y2，其顶点为E，设D为原抛物线y1对称轴上一点，当四边形BCDE为菱形时（按字母顺序构图），求y2的解析式．
2．如果两个连续偶数的积为288，那么这两个数的和为（　　）
A．34B．0C．-2D．34或-34
9．①（+1$\frac{1}{4}}$）×（-2.4）×（-0.125）；       
②0.1×（-100）×（-0.001）×（-10）×（-1000）×（-0.01）；
③（+2$\frac{8}{31}}$）×（-1$\frac{2}{7}}$）×（+2$\frac{1}{15}}$）×（-4$\frac{1}{2}}$）；
④（-375）×（-8）+（-375）×（-9）+375×（-7）．
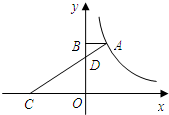6．如图，A是反比例函数y=$\frac{k}{x}$（k≠0）的图象上一点，点B、D在y轴正半轴上，△ABD是COD关于点D的位似图形，且△ABD与△COD的位似比为1：3，△ABD的面积为1，试求该反比例函数的解析式．
7．已知a，b是方程x2-1840x+1997=0的两根，（a2-1841a+1997）（b2-1841b+1997）=1997．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网