题目内容
9.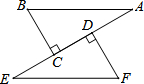 如图,AB=EF,BC⊥AE于C,FD⊥AE于D,CE=DA.求证:
如图,AB=EF,BC⊥AE于C,FD⊥AE于D,CE=DA.求证:(1)△ABC≌△EFD;
(2)AB∥EF.
分析 (1)由已知条件根据HL判定Rt△ABC≌Rt△EFD即可;
(2)由三角形全等的性质和平行线的判定证明即可.
解答 (1)证明:∵CE=DA,
∴AC=ED,
∵BC⊥AE于C,FD⊥AE于D,
在Rt△ABC与Rt△EFD中,
$\left\{\begin{array}{l}{AB=EF}\\{AC=ED}\end{array}\right.$,
∴Rt△ABC≌Rt△EFD;
(2)由(1)得 Rt△ACB≌Rt△EDF
∴∠A=∠E,
∴AB∥EF.
点评 主要考查全等三角形的判定,常用的判定方法有ASA,AAS,SSS,SAS,HL等.由平行线得到角相等是正确解答本题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
19.一辆公共汽车从起点站开出后,途中经过6个停靠站,最后到达终点站.下表记录了这辆公共汽车全程载客变化情况.
(1)中间第4站上车人数是1人,下车人数是7人;
(2)中间的6个站中,第6站没有人上车,第3站没有人下车;
(3)中间第二站开车时车上人数是24人,第五站停车时车上人数是22人;
(4)从表中你还能知道的一个信息是起点站上车21人.
| 停靠站 | 起点站 | 中间 第1站 | 中间 第2站 | 中间 第3站 | 中间 第4站 | 中间 第5站 | 中间 第6站 | 终点站 |
| 上下车人数 | +21 | -3 +8 | -4 +2 | 0 +4 | -7 +1 | -9 +6 | -7 0 | -12 |
(2)中间的6个站中,第6站没有人上车,第3站没有人下车;
(3)中间第二站开车时车上人数是24人,第五站停车时车上人数是22人;
(4)从表中你还能知道的一个信息是起点站上车21人.
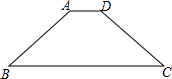 已知等腰梯形ABCD中,AD=3cm,BC=11cm,腰AB=5cm,点A为圆心,AD为半径的⊙A与底BC有怎样的位置关系?并说明理由.
已知等腰梯形ABCD中,AD=3cm,BC=11cm,腰AB=5cm,点A为圆心,AD为半径的⊙A与底BC有怎样的位置关系?并说明理由.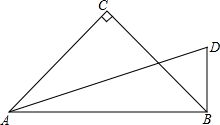 如图,已知AD=3,BD=1,AC=BC,∠C=∠ABD=90°,则BC=$\sqrt{5}$.
如图,已知AD=3,BD=1,AC=BC,∠C=∠ABD=90°,则BC=$\sqrt{5}$.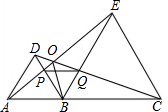 如图,已知点A、B、C在同一直线上,△ABD和△BCE都是等边三角形.则在下列结论中:①AP=DQ,②EP=EC,③PQ=PB,④∠AOB=∠BOC=∠COE.正确的结论是①③④(填写序号).
如图,已知点A、B、C在同一直线上,△ABD和△BCE都是等边三角形.则在下列结论中:①AP=DQ,②EP=EC,③PQ=PB,④∠AOB=∠BOC=∠COE.正确的结论是①③④(填写序号).
 如图,已知AB=AD,且AC平分∠BAD,求证:BC=DC.
如图,已知AB=AD,且AC平分∠BAD,求证:BC=DC.