题目内容
4．
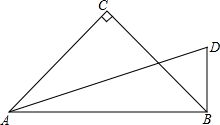如图，已知AD=3，BD=1，AC=BC，∠C=∠ABD=90°，则BC=$\sqrt{5}$．
分析 直接利用勾股定理得出AB的长，进而利用锐角三角函数关系求出BC的长．
解答 解：∵AD=3，BD=1，∠ABD=90°，
∴在Rt△ABD中，
AB=$\sqrt{A{D}^{2}-B{D}^{2}}$=$\sqrt{10}$，
∵AC=BC，∠C=90°，
∴AC=BC=ABsin45°=$\frac{\sqrt{2}}{2}$×$\sqrt{10}$=$\sqrt{5}$．
故答案为：$\sqrt{5}$．
点评 此题主要考查了勾股定理，正确利用勾股定理得出AB的长是解题关键．
练习册系列答案
相关题目
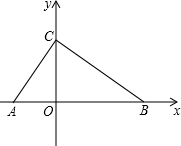已知：在平面直角坐标系中，点O为坐标原点，△ABC的顶点A（-2，0），点B、C分别在x轴正半轴上和y轴正半轴上，∠ACB=90°，∠BAC=60°．
15．三视图如图所示的几何体是（ ）
| A． | 三棱锥 | B． | 三棱柱 | C． | 四棱锥 | D． | 四棱柱 |
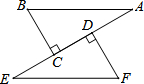如图，AB=EF，BC⊥AE于C，FD⊥AE于D，CE=DA．求证：
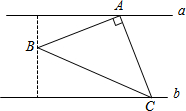如图，a∥b，点A在直线a上，点C在直线b上，∠BAC=90°，AB=AC，点B到a、b的距离分别为1和2，则△ABC的面积为5．
如图，AE⊥BC，DF⊥BC，E，F是垂足，且AE=DF，AB=DC，求证：∠ABC=∠DCB．