题目内容
4.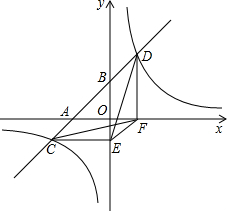 如图,一次函数y=ax+b的图象与x轴,y轴交于A,B两点,与反比例函数y=$\frac{k}{x}$的图象相交于C,D两点,分别过C,D两点作轴,轴的垂线,垂足为E,F,连结CF,DE,有下列结论:
如图,一次函数y=ax+b的图象与x轴,y轴交于A,B两点,与反比例函数y=$\frac{k}{x}$的图象相交于C,D两点,分别过C,D两点作轴,轴的垂线,垂足为E,F,连结CF,DE,有下列结论:①△CEF与△DEF的面积相等;②EF∥CD;③△DCE≌△CDF;④AC=BD;⑤△CEF的面积等于$\frac{k}{2}$,
其中正确的是①②④⑤.(填序号)
分析 此题要根据反比例函数的性质进行求解,解决此题的关键是要证出CD∥EF,可从①问的面积相等入手;△DFE中,以DF为底,OF为高,可得S△DFE=$\frac{1}{2}$|xD|•|yD|=$\frac{1}{2}$k,同理可求得△CEF的面积也是$\frac{1}{2}$k,因此两者的面积相等;若两个三角形都以EF为底,那么它们的高相同,即E、F到AD的距离相等,由此可证得CD∥EF,然后根据这个条件来逐一判断各选项的正误.
解答 解:设点D的坐标为(x,$\frac{k}{x}$),则F(x,0).
由函数的图象可知:x>0,k>0.
∴S△DFE=$\frac{1}{2}$DF•OF=$\frac{1}{2}$|xD|•|$\frac{k}{{x}_{D}}$|=$\frac{1}{2}$k,
同理可得S△CEF=$\frac{1}{2}$k,故⑤正确;
故S△DEF=S△CEF.故①正确;
若两个三角形以EF为底,则EF边上的高相等,故CD∥EF.故②正确;
③条件不足,无法得到判定两三角形全等的条件,故③错误;
④法一:∵CD∥EF,DF∥BE,
∴四边形DBEF是平行四边形,
∴S△DEF=S△BED,
同理可得S△ACF=S△ECF;
由①得:S△DBE=S△ACF.
又∵CD∥EF,BD、AC边上的高相等,
∴BD=AC,故④正确;
法2:∵四边形ACEF,四边形BDEF都是平行四边形,
而且EF是公共边,
即AC=EF=BD,
∴BD=AC,故④正确.
故答案为:①②④⑤.
点评 本题考查了反比例函数综合题,利用反比例函数的性质来证图形的面积相等,根据面积相等来证线段的平行或相等,设计巧妙,难度较大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.下列一元二次方程中有两个不相等的实数根的方程是( )
| A. | (x-1)2=0 | B. | x2+2x-19=0 | C. | x2+4=0 | D. | x2+x+l=0 |
12.若一元二次方程x2+2x+m=0没有实数根,则m的取值范围是( )
| A. | m≤$\frac{1}{2}$ | B. | m>1 | C. | m≤1 | D. | m<1 |
19.分式方程:$\frac{3}{2-x}$-$\frac{2x-5}{x-2}$=0的解是( )
| A. | x=-2 | B. | x=2 | C. | x=1 | D. | x=2或x=1 |
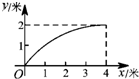
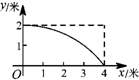
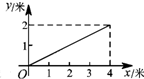
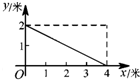
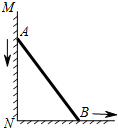 如图,一根长为5米的竹竿AB斜立于墙MN的右侧,底端B与墙角N 的距离为3米,当竹竿顶端A下滑x米时,底端B便随着向右滑行y米,反映y与x变化关系的大致图象是( )
如图,一根长为5米的竹竿AB斜立于墙MN的右侧,底端B与墙角N 的距离为3米,当竹竿顶端A下滑x米时,底端B便随着向右滑行y米,反映y与x变化关系的大致图象是( )